Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Why Does the DFT Need Windowing Functions?

September 1, 2023

Introduction

The blog describes why windowing functions are needed in spectral analysis! This blog uses the Fourier Transform as a Cross-Correlation as a foundation and shares much in common with the blog DFT Frequency Resolution Explained. Be sure to review those blog posts for a different perspective on this explanation.

More blogs!

Discrete Fourier Transform (DFT)

Before getting to windowing functions, it’s necessary to understand what the discrete Fourier transform (DFT) is and what the assumptions are regarding the inputs.

On page 542 (second edition) of Alan Oppenheim’s excellent book Discrete-Time Signal Processing [oppenheim1999] he makes the statement that the inputs to the DFT are assumed be periodic with period N,

(1) $\begin{equation*}x[n] = x[n+N].\end{equation*}$

Why? Where does this requirement come from?

The DFT is a series of cross-correlations with an input signal $x[n]$ and complex sinusoids $e^{j2\pi kn/N}$ ,

(2) $\begin{equation*}X[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N}.\end{equation*}$

The complex sinusoid $e^{-j2\pi kn/N}$ has a period of N such that

(3) $\begin{equation*}e^{-j2\pi kn/N} = e^{-j2\pi k(n+N)/N}.\end{equation*}$

Figure 1 shows how the complex sinusoid

(4) $\begin{equation*}x[n] = e^{j2\pi (3/256)n}\end{equation*}$

is periodic in the time domain.

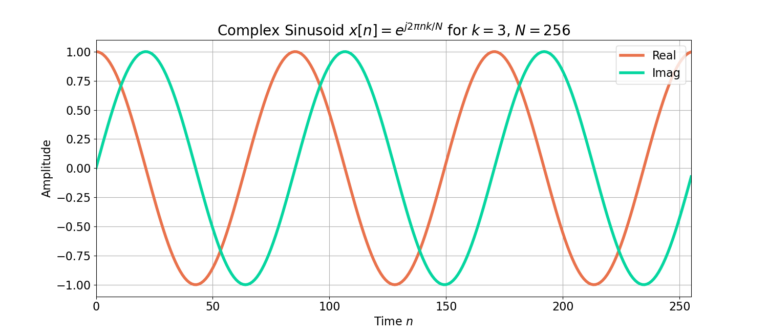
The inputs to the DFT are assumed to be periodic in N because the complex sinusoids used in the cross-correlation are periodic in N. Cross-correlation is a measure of similarity. The highest measure of similarity of a complex exponential with period N is also a complex sinusoid with period N. Therefore the DFT measures the similarity of an input signal with those periodic complex exponentials.

Periodic Inputs

The implication of the periodicity for an input signal is that the beginning and end of a time-series is connected. Begin with a signal $x[n]$ of length N, such that N samples of the time-series for $0 \le n \le N-1$ ,

(5) $\begin{equation*}x[0], x[1], x[2], ~\dots, x[N-2], x[N-1].\end{equation*}$

The other samples for $n < 0$ and $n > N-1$ can derived from the periodicity constraint (1). The values $x[-2]$ and $x [-1]$ can be written such that

(6) $\begin{equation*}x[-2] = x[-2+N] = x[N-2],\end{equation*}$

(7) $\begin{equation*}x[-1] = x[-1+N] = x[N-1].\end{equation*}$

The values $x[N]$ and $x[N+1]$ can be written such that

(8) $\begin{equation*}x[N] = x[0+N] = x[0],\end{equation*}$

(9) $\begin{equation*}x[N+1] = x[1+N] = x[1].\end{equation*}$

The time-series x[n] can therefore be written as

(10) $\begin{equation*}\dots, x[N-2], x[N-1], x[0], x[1 ], x[2], ~\dots, x[N-2], x[N-1], x[0], x[1], ~\dots\end{equation*}$

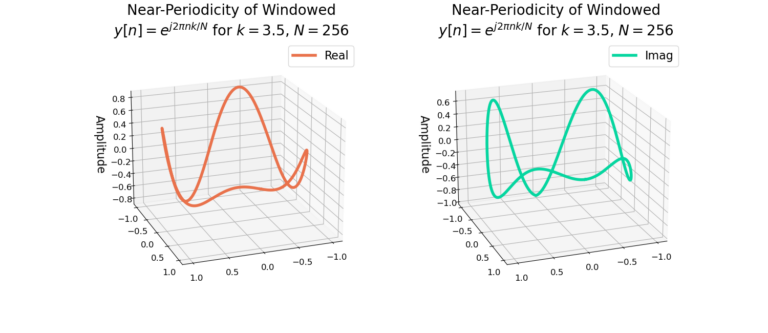
which shows how the last sample x[N-1] is immediately followed by the first sample x[0], connecting the first and last sequence of the time-series. Figure 2 gives a graphical example in 3D, showing how a periodic signal begins and ends at the sample sample.

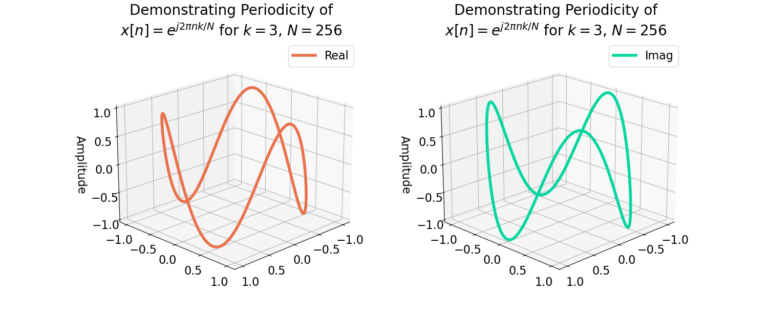
Thus periodic inputs are assumed, but not required, for the DFT. What happens when the input is not periodic? A windowing function is needed.

Windowing Functions

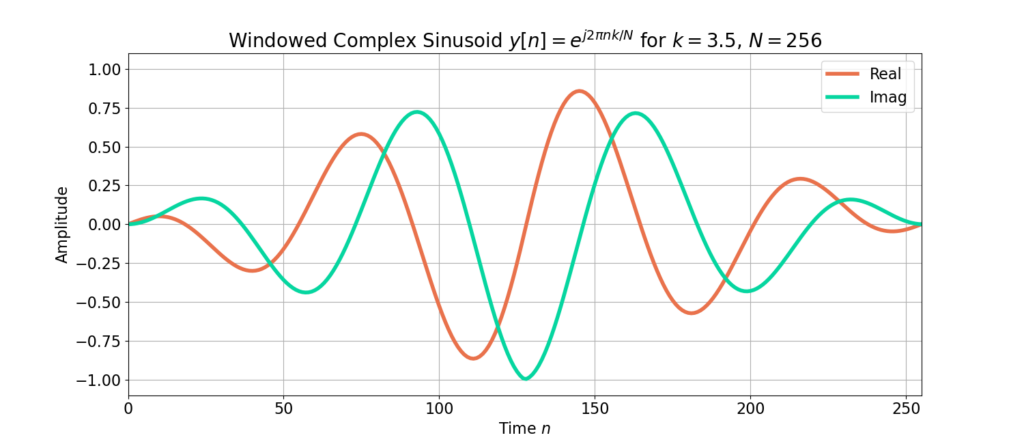
The complex sinusoid with $k=3.5$ and $N=256$ ,

(11) $\begin{equation*}y[n] = e^{j2\pi (3.5/256)n}\end{equation*}$

does not meet the periodicity constraint in (1) which is displayed in Figure 3.

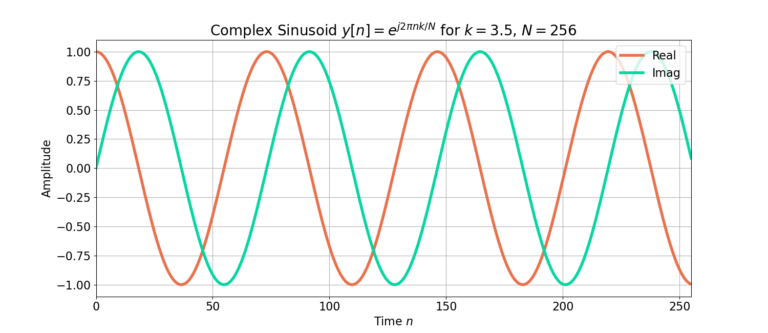
Figure 4 more clearly demonstrates how there is a sharp transition between the beginning and ending samples of the complex sinusoid $y[n]$ .

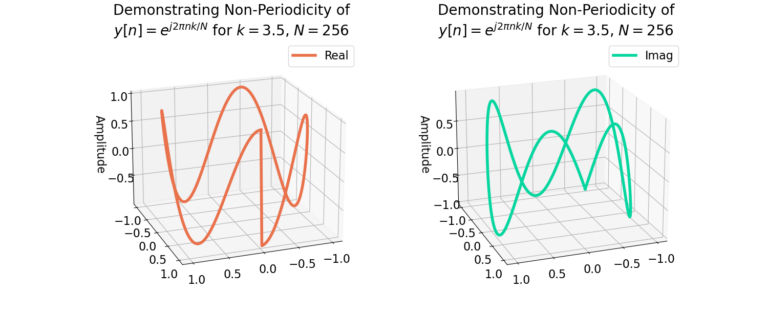
Windowing functions force a periodicity of length N in the time-series x[n] by driving the inputs to zero at the beginning and ending samples. Figure 5 and Figure 6 demonstrate how the sharp transitions are smoothed by the application of the Bartlett window. Notice how the sharp transitions from Figure 4 have been smoothed by the windowing function in Figure 6.

Conclusion

The DFT requires periodic inputs because it acts as a cross-correlator with a complex sinusoid. The inputs are assumed to periodic in that the last sample connects to the first input sample without a sharp transition as demonstrated with 3D plots. A windowing function forces a non-periodic input to appear periodic by driving the beginning and ending samples to zero.

More blogs!

2 Responses

Dylan Gormley says:

October 4, 2023 at 12:47 pm

Hey, Matt! It’s been a while! I just found your blog. This is such a great explaination!

Reply
1. WaveWalkerDSP says:
  
  October 10, 2023 at 8:43 pm
  
  Thank you! It’s good to hear from you Dylan
  
  Reply

Wave Walker DSP

DSP Algorithms for RF Systems

Trending