Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Fourier Transform Explanation as a Cross-Correlation

December 22, 2021

Introduction

For years I accepted the Fourier transform equation on faith without knowing where it came from or why it worked. Were you in the same situation? Are you there now? In this post I describe how the Fourier transform is the cross correlation between a signal x(t) and a complex exponential $e^{j 2 \pi f t }$ . The Fourier transform explanation begins by reviewing cross correlation and then applies it to a complex exponential derive the continuous time and discrete time Fourier transform.

You might enjoy these other blogs on cross-correlation:

Cross Correlation

Recall that cross correlation is a measure of similarity. The cross correlation of x(t) and y(t) gives a mathematical measure of similarity between the two signals at different relative time delays $\tau$ , also called time lags, which is given by

(1) $\begin{equation*}R_{xy}(\tau) = \int_{-\infty}^{\infty} x(t)y^*(t-\tau) ~ dt.\end{equation*}$

Similarly for discrete-time sequences the cross correlation of x[n] and y[n] is given by

(2) $\begin{equation*}R_{xy}[\tau] = \sum_{n=-\infty}^{\infty} x[n]y^*[n-\tau].\end{equation*}$

Continuous Time Fourier Transform Explanation

The Fourier transform $X(f) = \mathcal{F}\{ x(t) \}$ describes the frequency content in x(t) at frequency f. In order to analyze the frequency content in x(t) at frequency f it is correlated with a complex exponential $e^{j2\pi ft}$ . Substituting

(3) $\begin{equation*}y(t) = e^{j2\pi f t},\end{equation*}$

the Fourier transform can be written as a correlation (1)

(4) $\begin{equation*}\begin{split}R_{xy}(\tau) & = \int_{-\infty}^{\infty} x(t)y^*(t-\tau) ~ dt \\& = \int_{-\infty}^{\infty} x(t) e^{-j2\pi f (t-\tau)} ~ dt.\end{split}\end{equation*}$

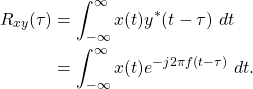
The complex exponential (3) is periodic and defined over all time t, therefore computing (4) over multiple time lags does not provide any new information. Therefore, (4) can be evaluated at $\tau=0$ ,

(5) $\begin{equation*}R_{xy}(0) = \int_{-\infty}^{\infty} x(t) e^{-j2\pi f t} ~ dt\end{split}\end{equation*}$

which is the Fourier transform

(6) $\begin{equation*}X(f) = \mathcal{F} \{ x(t) \} = \int_{-\infty}^{\infty} x(t) e^{-j2\pi f t} ~ dt.\end{split}\end{equation*}$

Discrete Time Fourier Transform Explanation

The discrete-time Fourier transform (DTFT) is the discrete-time counterpart to the Fourier transform. Where the Fourier transform operates on continuous time signals the DTFT operates on discrete-time sequences. Similar to the continuous time Fourier transform above, the DTFT can be derived by using the cross correlation in (2) and substituting

(7) $\begin{equation*}y[n] = e^{j\omega n}\end{equation*}$

where $\omega = 2\pi f/f_s$ and $f_s$ is the sampling frequency. The cross correlation(2) of time-series x[n] with the complex exponential y[n] (7) is given by

(8) $\begin{equation*}\begin{split}R_{xy}[\tau] & = \sum_{n=-\infty}^{\infty} x[n] b^*[n-\tau] \\& = \sum_{n=-\infty}^{\infty} x[n] e^{-j \omega \left( n-\tau \right) }.\end{split}\end{equation*}$

Evaluating (8) at $\tau=0$ ,

(9) $\begin{equation*}R_{xy}[0] = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n }\end{equation*}$

leads to the discrete-time Fourier transform

(10) $\begin{equation*}X(e^{j\omega}) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n }.\end{equation*}$

Conclusion

The Fourier transform, both continuous-time and discrete-time, is the cross-correlation with an infinitely long complex exponential. The Fourier transform can be derived by calculating cross-correlation with a complex exponential at the time lag $\tau=0$ .

You might enjoy these other blogs on cross-correlation:

If you liked this post you might like the List of Important Math for DSP!

Wave Walker DSP

DSP Algorithms for RF Systems

Trending

Buy the Book!

Table of Contents

Introduction

Cross Correlation

Continuous Time Fourier Transform Explanation

Discrete Time Fourier Transform Explanation

Conclusion

Related

Leave a ReplyCancel reply