Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Cross Correlation Explained With Real Signals

December 1, 2021

Introduction

Cross correlation mathematically measures the similarity of signals. Consider an example where you have a set of data samples represented by x[n] and y[n]. Cross correlation is used to measure on a sample by sample basis how similar x[n] is to y[n]. Simple examples with plots will demonstrate different combinations of positive, negative, strong and weak correlations.

Correlation Function

Correlation for DSP engineers, referred to as cross-correlation, is slightly different than the equation used by statisticians and mathematicians but they share the same underlying principles. The cross-correlation of sequences x[n] and y[n] is given by [gardner1988, p.212]

(1) $\begin{equation*}R_{xy}[\tau] = \sum_{n} x[n] y^*[n-\tau].\end{equation*}$

The term $\tau$ is referred to as the “time-lag” and controls the relative time delay between the two sequences. The cross-correlation (1) at $\tau=0$ calculates the similarity when there is no relative time delay,

(2) $\begin{equation*}R_{xy}[0] = \sum_{n} x[n] y^*[n].\end{equation*}$

A special case of the cross-correlation is when x[n] = y[n] is referred to as autocorrelation,

(3) $\begin{equation*}R_{x}[\tau] = \sum_{n} x[n] x^*[n-\tau].\end{equation*}$

A large correlation value means the sequences x[n] and y[n] are similar while a large negative correlation means the sequences are similar but have opposite polarity. Small correlation values means the sequences have weak similarity while a correlation of 0 means the sequences have no similarity.

Strong Positive Correlation

Consider a sequence

(4) $\begin{equation*}x_{0}[n] = \begin{cases}1, & n = 0 \\-1, & n = 1 \\1, & n = 2 \\-1, & n = 3 \\0, & \text{otherwise.}\end{cases}\end{equation*}$

The sequence $x_{0}[n]$ autocorrelates at $\tau=0$ (2) according to

(5) $\begin{equation*}\begin{split}R_{x_{0}}[0] & = \sum_{n} x_{0}[n] x_{0}^*[n] \\& = \left( 1 \cdot 1 ) + (-1 \cdot -1) + (1 \cdot 1 ) + (-1 \cdot -1) \\& = 4.\end{split}\end{equation*}$

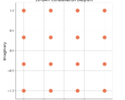
Figure 1 shows that the two sequences are identical at $\tau = 0$ (no relative time delay) and therefore they should have the maximum correlation value, which in this case is 4. The larger the correlation, the larger the similarity.

Strong Negative Correlation

Consider a sequence which is the negative of $x_{0}[n]$ ,

(6) $\begin{equation*}x_{1}[n] = -x_{0}[n]\end{equation*}$

such that

(7) $\begin{equation*}x_{1}[n] = \begin{cases}-1, & n = 0 \\1, & n = 1 \\-1, & n = 2 \\1, & n = 3 \\0, & \text{otherwise.}\end{cases}\end{equation*}$

The cross-correlation between $x_{0}[n]$ and $x_{1}[n]$ at $\tau=0$ from (2) is

(8) $\begin{equation*}\begin{split}R_{x_{0}x_{1}}[0] & = \sum_{n} x_{0}[n] x_{1}^*[n] \\& = \left( 1 \cdot -1 ) + (-1 \cdot 1) + (1 \cdot -1 ) + (-1 \cdot 1) \\& = -4.\end{split}\end{equation*}$

A negative correlation value means that the two sequences are similar at $\tau = 0$ (no relative time delay) but have opposite polarity. Figure 2 shows that the two sequences are the same with opposite polarity which is why the cross-correlation in (8) is the maximum negative value, -4.

Weak Positive Correlation

Consider a sequence $x_{2}[n]$ which has 1 data point in difference from $x_{0}[n]$ such that

(9) $\begin{equation*}x_{2}[n] =\begin{cases}-1, & n = 0 \\-1, & n = 1 \\1, & n = 2 \\-1, & n = 3 \\0, & \text{otherwise.}\end{cases}\end{equation*}$

The cross-correlation between $x_{0}[n]$ and $x_{2}[n]$ at $\tau=0$ from (2) is

(10) $\begin{equation*}\begin{split}R_{x_{0}x_{2}}[0] & = \sum_{n} x_{0}[n] x_{2}^*[n] \\& = \left( 1 \cdot -1 ) + (-1 \cdot -1) + (1 \cdot 1 ) + (-1 \cdot -1) \\& = 2.\end{split}\end{equation*}$

A weak correlation value of 2 in (10) as compared to 4 in (5) means that the two sequences share some similarity at $\tau = 0$ but are not the exact same. Figure 3 shows that the two sequences are similar but with a single difference at n=0 which is why the cross-correlation in (10) is only 2.

Weak Negative Correlation

Consider a sequence $x_{3}[n]$ which has 1 data point the same as $x_{0}[n]$ but the other 3 are opposite polarity such that

(11) $\begin{equation*}x_{3}[n] =\begin{cases}-1, & n = 0 \\1, & n = 1 \\-1, & n = 2 \\-1, & n = 3 \\0, & \text{otherwise.}\end{cases}\end{equation*}$

The cross-correlation between $x_{0}[n]$ and $x_{3}[n]$ at $\tau=0$ from (2) is

(12) $\begin{equation*}\begin{split}R_{x_{0}x_{3}}[0] & = \sum_{n} x_{0}[n] x_{3}^*[n] \\& = \left( 1 \cdot -1 ) + (-1 \cdot 1) + (1 \cdot -1 ) + (-1 \cdot -1) \\& = -2.\end{split}\end{equation*}$

A weak negative correlation value of -2 means that the two sequences share some similarity at $\tau = 0$ with opposite polarity but are not the exact same. Figure 4 shows that the two sequences are similar but with a single sample at n=3 in common, while the other three samples at n=0, 1, 2 are the opposite polarity which is why the cross-correlation in (12) is only -2.

Conclusion

Correlation is a way to mathematically measure similarity of two sequences. A large positive correlation means the two sequences are similar whereas a large negative correlation means the two sequences are similar but have opposite polarity. A small correlation value, positive or negative, means the two sequences share few similarities. A correlation value of zero means the two sequences do not share any similarities.

This post covered a subset of the cross-correlation, only for $\tau=0$ , in order to simplify the examples in this introduction. A future blog post will describe why the cross-correlation is computed over all time lags $\tau$ and how cross-correlation is applied in DSP algorithms.