Trending
![Figure 1: The weights of the partitioned half band filter hA[n] and hB[n].](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAH0AAABLAQAAAAB12LU4AAAAAnRSTlMAAHaTzTgAAAASSURBVDjLY2AYBaNgFIyCEQcABPsAAZzw+UwAAAAASUVORK5CYII=) Polyphase Half Band Filter for Decimation by 2 posted on September 29, 2021
Polyphase Half Band Filter for Decimation by 2 posted on September 29, 2021 Half Band Filter Design Function in Python posted on December 8, 2021
Half Band Filter Design Function in Python posted on December 8, 2021 Introduction to Interpolation and Upsampling posted on September 1, 2022
Introduction to Interpolation and Upsampling posted on September 1, 2022 Half Band Filter Design: Exceptional Filtering Efficiency! posted on September 27, 2021
Half Band Filter Design: Exceptional Filtering Efficiency! posted on September 27, 2021 Power and Energy in Discrete-Time Signals posted on December 1, 2023
Power and Energy in Discrete-Time Signals posted on December 1, 2023 The Almanack of Naval Ravikant: Buy The Book Now! posted on January 12, 2022
The Almanack of Naval Ravikant: Buy The Book Now! posted on January 12, 2022 FIR Low Pass Filter Design with Remez posted on September 22, 2021
FIR Low Pass Filter Design with Remez posted on September 22, 2021![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAH0AAABLAQAAAAB12LU4AAAAAnRSTlMAAHaTzTgAAAASSURBVDjLY2AYBaNgFIyCEQcABPsAAZzw+UwAAAAASUVORK5CYII=) Calculate Signal to Noise Ratio (SNR) in Python Simulation posted on July 1, 2024
Calculate Signal to Noise Ratio (SNR) in Python Simulation posted on July 1, 2024 Designing an FIR Band Pass Filter with Remez posted on September 24, 2021
Designing an FIR Band Pass Filter with Remez posted on September 24, 2021 Product to Sum Trigonometric Identities with Euler’s Formula posted on June 15, 2022
Product to Sum Trigonometric Identities with Euler’s Formula posted on June 15, 2022
Recent Blogs


Apollo 13 and Engineering Operations
February 1, 2025
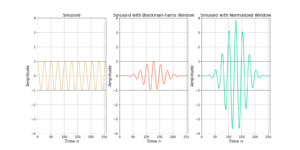
Windowing Function Gain Normalization
January 1, 2025

Should I Get a Masters Degree?
December 1, 2024

What DSP Classes Should I Take?
November 1, 2024

How To Install GNU Radio Source Code
October 1, 2024

How to Travel Well At the Airport
September 1, 2024

Celebrating Three Years of WWDSP!
August 28, 2024

How to Count in Binary Numbers
August 1, 2024
![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/2023/12/HowToComputeSignalToNoiseRatioSNRInSimulation_signalNoiseTimeDomain-300x240.png)
New book!
Now for sale: The third edition of DSP for Beginners: Simple Explanations for Complex Numbers! Includes a new chapter on sampling.
Receive Blogs via Email
DSP Resources
For everything there is a season, and a time for every matter under heaven. A time to cast away stones, and a time to gather stones together. A time to embrace, and a time to refrain from embracing. Ecclesiastes 3:1,5
The earth was without form and void, and darkness was over the face of the deep. And the Spirit of God was hovering over the face of the waters. Genesis 1:2
Behold, I am toward God as you are; I too was pinched off from a piece of clay. Job 33:6
Enter His gates with thanksgiving, and His courts with praise! Give thanks to Him; bless His name! Psalm 100:4
Lift up your hands to the holy place and bless the Lord! Psalm 134:2
Blessed is the man who trusts in the Lord, whose trust is the Lord. He is like a tree planted by water, that sends out its roots by the stream, and does not fear when heat comes, for its leaves remain green, and is not anxious in the year of drought, for it does not cease to bear fruit. Jeremiah 17:7-8
He said to him, “You shall love the Lord your God with all your heart and with all your soul and with all your mind. This is the great and first commandment. And a second is like it: You shall love your neighbor as yourself. On these two commandments depend all the Law and the Prophets.” Matthew 22:37-39
Then He said to me, “Prophesy over these bones, and say to them, O dry bones, hear the word of the Lord. Thus says the Lord God to these bones: Behold, I will cause breath to enter you, and you shall live." Ezekiel 37:4-5
Riches do not profit in the day of wrath, but righteousness delivers from death. Proverbs 11:4
The angel of the Lord appeared to him in a flame of fire out of the midst of a bush. He looked, and behold, the bush was burning, yet it was not consumed. And Moses said, “I will turn aside to see this great sight, why the bush is not burned.” When the Lord saw that he turned aside to see, God called to him out of the bush, “Moses, Moses!” And he said, “Here I am.” Exodus 3:2-3
Daniel answered and said: “Blessed be the name of God forever and ever, to whom belong wisdom and might. He changes times and seasons; He removes kings and sets up kings; He gives wisdom to the wise and knowledge to those who have understanding." Daniel 2:20-21
Now the Lord is the Spirit, and where the Spirit of the Lord is, there is freedom. 2 Corinthians 3:17
This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.
© 2021-2025 Wave Walker DSP
![Figure 1: The weights of the partitioned half band filter hA[n] and hB[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/2226-featured-125x75.png)



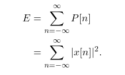


![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x75.png)