Table of Contents
Introduction
This blog derives the ideal low pass filter (LPF) step by step using simple math.
More DSP blogs!
Frequency Domain Ideal Low Pass Filter
An ideal low pass filter (LPF) allows signals below the cutoff frequency 
to pass through unmodified with a linear gain of 1 and no phase change, while simultaneously completely rejecting all frequencies above the cutoff frequency with a linear gain of 0.
Mathematically, the ideal LPF is defined in the frequency domain by [oppenheim1999, p.43]
(1) 
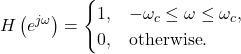
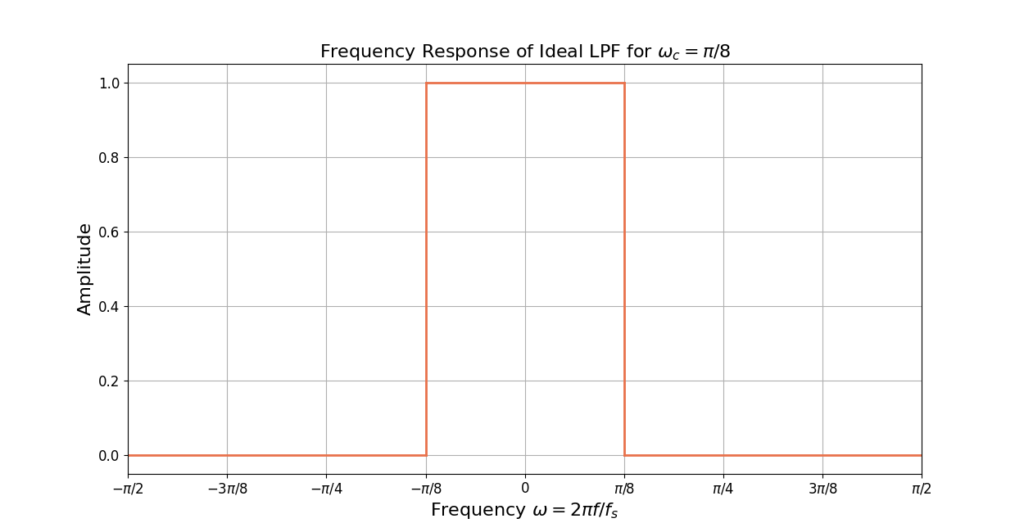
The frequency response for the ideal LPF in (1) for 
is given in Figure 1.
Time Domain Ideal Low Pass Filter
The ideal LPF in the time domain is derived by taking the inverse discrete-time Fourier transform (IDTFT) of (1),
(2) ![\begin{equation*}h[n] = \mathcal{F}^{-1} \left\{ H\left( e^{j\omega} \right) \right\}.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-2c076b16eb939298d22c39df8cd558c9_l3.png "Rendered by QuickLaTeX.com")
The IDTFT is defined as
(3) ![\begin{equation*}x[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} X\left( e^{j\omega} \right) e^{j\omega n}d\omega.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-8dafb7a6e93c5b4cf10be9339c4f08d1_l3.png "Rendered by QuickLaTeX.com")
(4) ![\begin{equation*}h[n] = \frac{1}{2\pi} \int_{-\omega_c}^{\omega_c} e^{j\omega n} d\omega.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-28659a66d16e12635c5590478810e4b1_l3.png "Rendered by QuickLaTeX.com")
The integral in (4) is simplified via Euler’s formula as
(5) ![\begin{equation*}\begin{split}h[n] & = \frac{1}{j2\pi n} e^{j \omega n} \Big|_{-\omega_c}^{\omega_c} \\& = \frac{1}{j2\pi n} \left( e^{j\omega_c n} - e^{-j\omega_c n} \right) \\& = \frac{1}{\pi n} \sin \left( \omega_c n \right). \\\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-41452002ff4da11d2c1cd60a5f820ad7_l3.png "Rendered by QuickLaTeX.com")
The cutoff frequency is the frequency in radians, defined as
(6) 
where 
is the frequency 
in Hz normalized by the sampling rate 
,
(7) 
The impulse response h[n] can therefore be written as
(8) ![\begin{equation*}h[n] = \frac{1}{\pi n} \sin \left( 2\pi f_{n} n \right).\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-1846e7e60d74b08bfa9debf87f3498fa_l3.png "Rendered by QuickLaTeX.com")
Equation (8) can then be transformed into a sinc function where
(9) 
The impulse response h[n] can therefore be written as
(10) ![\begin{equation*}\begin{split}h[n] & = \frac{1}{\pi n} \sin \left( 2 \pi f_n n \right) \\& = \frac{2 f_n}{2 f_n \pi n} \left( 2 \pi f_n n \right) \\& = 2 f_n \text{sinc} \left( 2 f_n n \right) \\\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-2b3866dc14927abe96bfef70840997b6_l3.png "Rendered by QuickLaTeX.com")
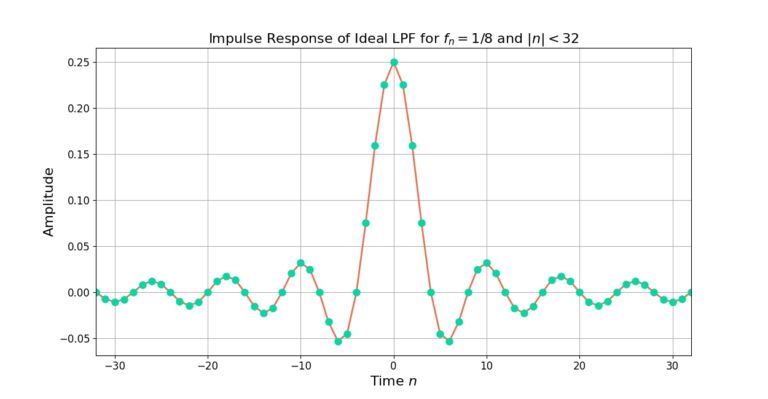
The impulse response from (10) is given in Figure 2.
Conclusion
The ideal low pass filter is a finite-length rectangle in the frequency domain but an infinitely long sinc in the time domain. Selecting the cutoff frequency determines which frequencies will be passed by the filter and which will be attenuated.
More DSP blogs!