Table of Contents
Introduction
Easy guide on interpolation! Describes upsampling and how to build the appropriate low pass filter. A sine wave is used for clarity but this applies to all discrete-time signals.
More DSP blogs!
Interpolation Overview
Interpolation in the process of increasing the number of samples between two known data points. Interpolation in DSP increases the number of samples between discrete-time samples through the process of upsampling and low pass filtering. Interpolation increases the sampling rate for a signal such that a signal will appear to be sampled at a higher frequency.
Figure 1 shows the same sine wave with two sampling rates. Interpolation by 5 increases the number of samples, from 15 samples in low sampling rate sine wave to 125 samples in the high sampling rate sine wave.
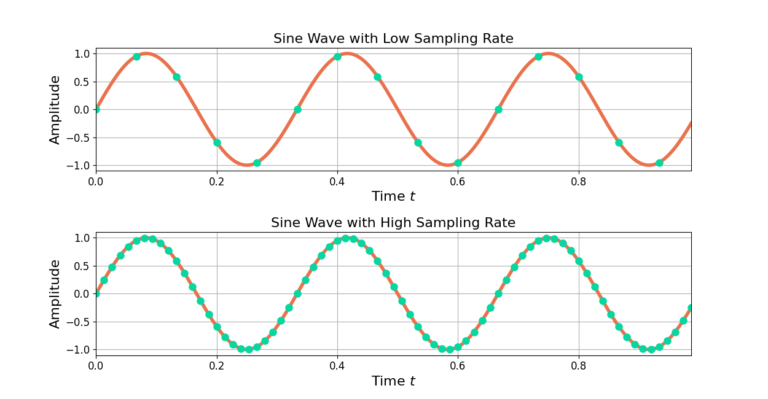
Interpolation is a two step process: upsampling followed by low pass filtering.
Upsampling
Upsampling is the process of zero-padding a time-series. Upsampling by M increases the number of samples by M through inserting M-1 zero samples after each input sample. Figure 2 shows the low sample rate sine wave being upsampled by 5. Each sample is followed by 4 zeros.
Increasing the number of output samples for every 1 input sample increases the sample rate. Increasing the number of samples by 5 equivalently increases the sampling rate by a factor of 5.
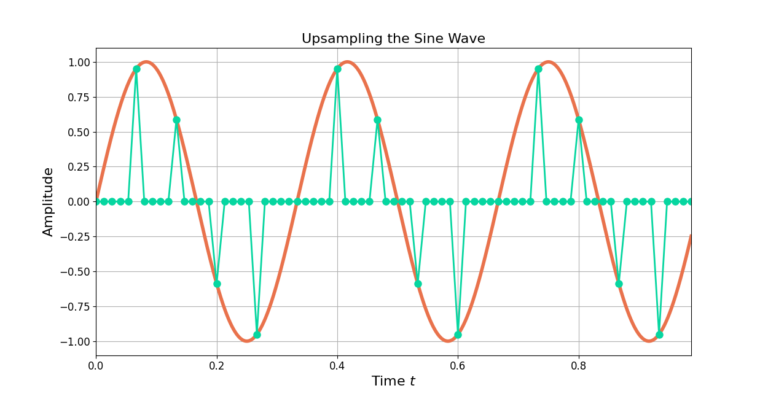
The zeros in Figure 2 need to be smoothed using a low pass filter.
Low Pass Filtering
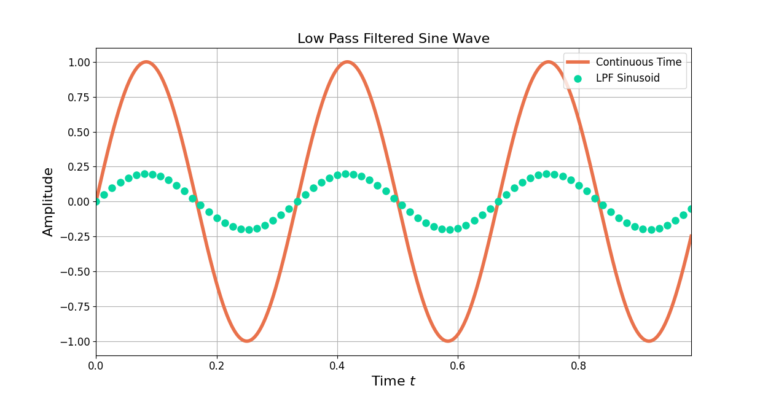
Low pass filtering is needed to smooth the zero-padded signal to fill in the gaps between the non-zero samples. A low pass filter is designed with a cut-off frequency of
(1) ![]()
where ![]() is the sampling rate and M is the interpolation factor [oppenheim1999, p.173]. Figure 3 shows the result after low pass filtering with a Remez-designed filter from this blog post with a normalized cutoff frequency of
is the sampling rate and M is the interpolation factor [oppenheim1999, p.173]. Figure 3 shows the result after low pass filtering with a Remez-designed filter from this blog post with a normalized cutoff frequency of ![]() where M=5.
where M=5.
Scipy’s remez() designs filters with 0 dB gain, or a linear gain of 1. The zero-padding due to the upsampling reduces the average signal level of the sinusoid, therefore a gain of M=5 is applied to the signal. The filter is also designed to have an odd-length to avoid a non-integer delay in the filter output.
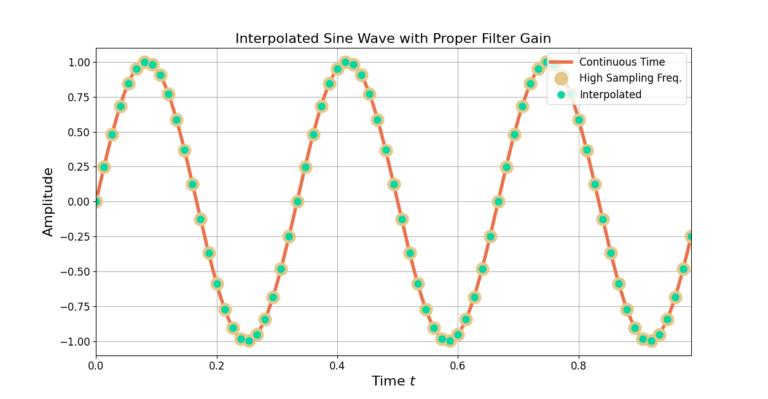
Figure 5 shows how the samples of the complex sinusoid sampled at a higher rate overlaps with the samples of the interpolated complex sinusoid which started with a lower sampling rate.
Conclusion
Interpolation is a two step process: upsampling and low pass filtering. The LPF must have a cutoff frequency of ![]() and a gain of M when interpolating by a factor of M.
and a gain of M when interpolating by a factor of M.
More DSP blogs!

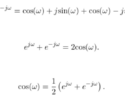
![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-125x100.png)






3 Responses
Thank you–this was just what I needed! Such a clear, simple explanation!
Wouldn’t upsampling also require a PLL?
Good question. Interpolation by itself does not require a PLL (phase locked loop). Interpolation is the process of increasing the number of samples used to represent a discrete-time signal; increasing the sample density in a sense. In the frequency domain this changes the proportion of the available bandwidth the signal occupies. The larger the interpolation rate the smaller the ratio of the signal’s bandwidth to the sampling rate. Within the RF world a PLL is used to track (or synchronize to) a signal’s carrier frequency and/or phase. These two operations, interpolation and PLL, are disjoint from one another and can be applied independent of one another. I hope this helps. Please let me know if you have any more questions.