Table of Contents
Introduction
The focus of this blog is to describe the low pass filter design process with the remez() function, which is one of many ways to create FIR filter weights. The filter parameters of:
- filter length,
- pass-band,
- stop-band,
- cut-off frequency,
- transition bandwidth,
- and sidelobe attenuation
will be discussed, including their impact on the frequency response and how their trade-offs effect the design.
I’d also suggest taking a look at fred harris’ Multirate Signal Processing text [harris2021, p.55-82] which has a great chapter on the Remez algorithm.
More blog posts on filter design:
scipy.signal.remez()
The Remez design function can be found in the Python scipy package. The description can be found here: https://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.remez.html
The function call is
scipy.signal.remez(numtaps, bands, desired, weight=None, Hz=None, type='bandpass', maxiter=25, grid_density=16, fs=None)
The three parameters of interest for now are numtaps, bands and desired. The parameter numtaps is simply the length of the filter.
The bands parameter and desired parameter work together to describe the frequencies and amplitudes of the filter’s magnitude response. Figure 1 gives an example of how the bands and desired parameters can be set for a low-pass filter. For the low-pass case, the values bands[1] is referred to as the pass-band frequency and bands[2] as the stop-band frequency.
The focus of this blog is to describe the low pass filter design process with the remez() function, which is one of many ways to create FIR filter weights. The filter parameters of:
- filter length,
- pass-band,
- stop-band,
- cut-off frequency,
- transition bandwidth,
- and sidelobe attenuation
will be discussed, including their impact on the frequency response and how their trade-offs effect the design.
I’d also suggest taking a look at fred harris’ Multirate Signal Processing text [harris2021, p.55-82] which has a great chapter on the Remez algorithm.
More blog posts on filter design:
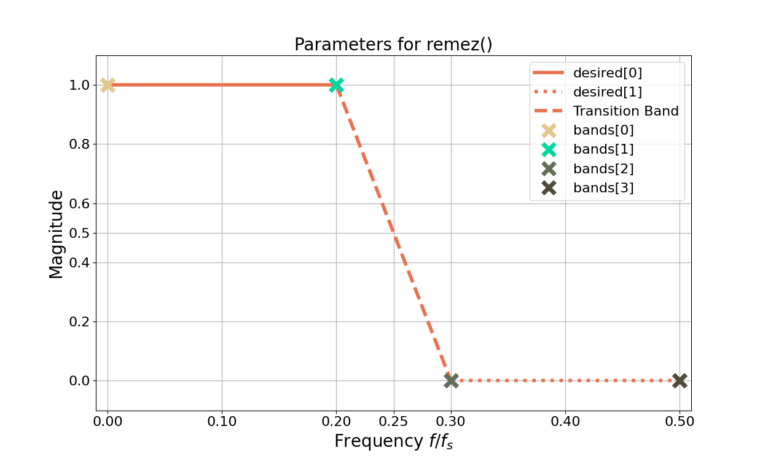
The bands define the edges of the response as a frequency vector, named freqVec below and where desired sets the amplitude of the response, named ampVec. The code for the filter parameters in Figure 1 is as follows:
import scipy.signal
filterLength = 21
fPass = 0.2
fStop = 0.3
freqVector = [0, fPass, fStop, 0.5]
ampVector = [1, 0]
remezFilter = scipy.signal.remez(filterLength,freqVector,ampVector)
Example FIR Low Pass Filter Design
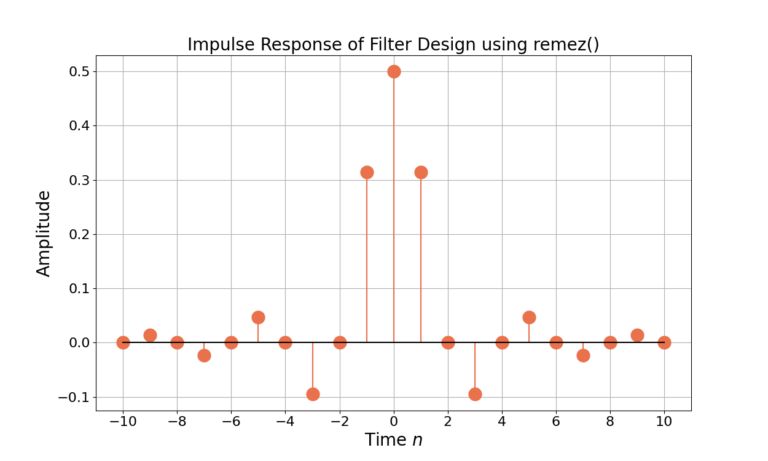
Starting with a filter length (numtaps) of 21 will make it easier to see how the other parameters effect the filter frequency response. Running the code creates a filter with the impulse response in Figure 2 and frequency response in Figure 3. The impulse response in Figure 2 correctly shows 21 total weights which is the desired length of the filter numtaps.
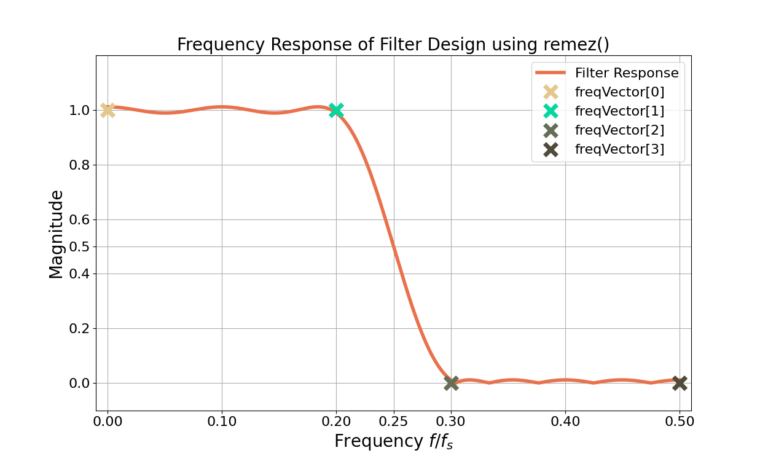
As expected the designed magnitude response in Figure 3 goes approximately through the locations defined by both freqVec and ampVec. The magnitude of a frequency response is typically viewed in decibels, through the relationship
(1) ![]()
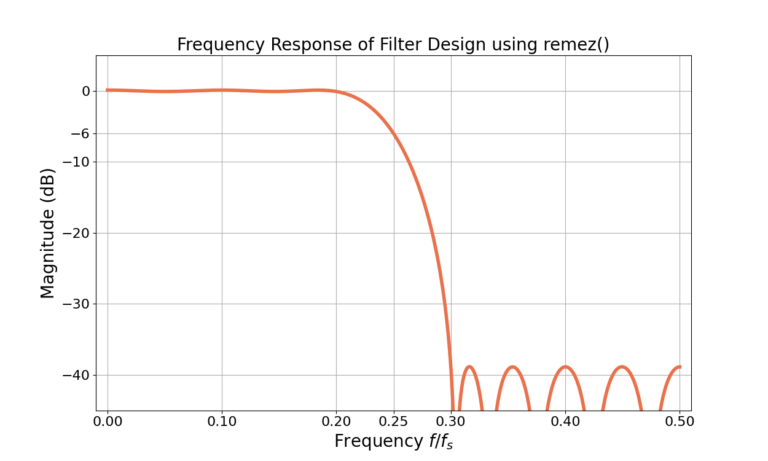
where ![]() is the frequency response. Note that when the magnitude in the frequency domain is displayed it is most commonly the magnitude-squared as in (1), as in Figure 4.
is the frequency response. Note that when the magnitude in the frequency domain is displayed it is most commonly the magnitude-squared as in (1), as in Figure 4.
Designing with Cut-off Frequency and Transition Bandwidth
An alternative to designing the filter based on the pass-band and stop-band frequencies is defining a cut-off frequency and a transition bandwidth. The transition bandwidth is the difference between the stop-band frequency and the pass-band frequency. The cut-off frequency is typically designed to be at a magnitude of (equivalently) 0.5 in linear magnitude, 3 dB in dB-magnitude, or 6 dB in dB-magnitude squared. Note that the filter frequency response passes through each of these points in Figure 1, Figure 3 and Figure 4.
The code for designing based on the cutoff frequency is as follows:
import scipy.signal
filterLength = 21
fCutoff = 0.25
fTransitionBandwidth = 0.1
fPass = fCutoff - (fTransitionBandwidth/2)
fStop = fCutoff + (fTransitionBandwidth/2)
freqVector = [0, fPass, fStop, 0.5]
ampVector = [1, 0]
remezFilter = scipy.signal.remez(filterLength,freqVector,ampVector)
Effects of Low Pass Filter Parameters
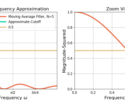
What happens when the cut-off frequency is changed? Figure 5 gives three examples for different cutoff frequencies with the same transition bandwidth and filter length. Figure 6 zooms into the pass-band of the same filters.
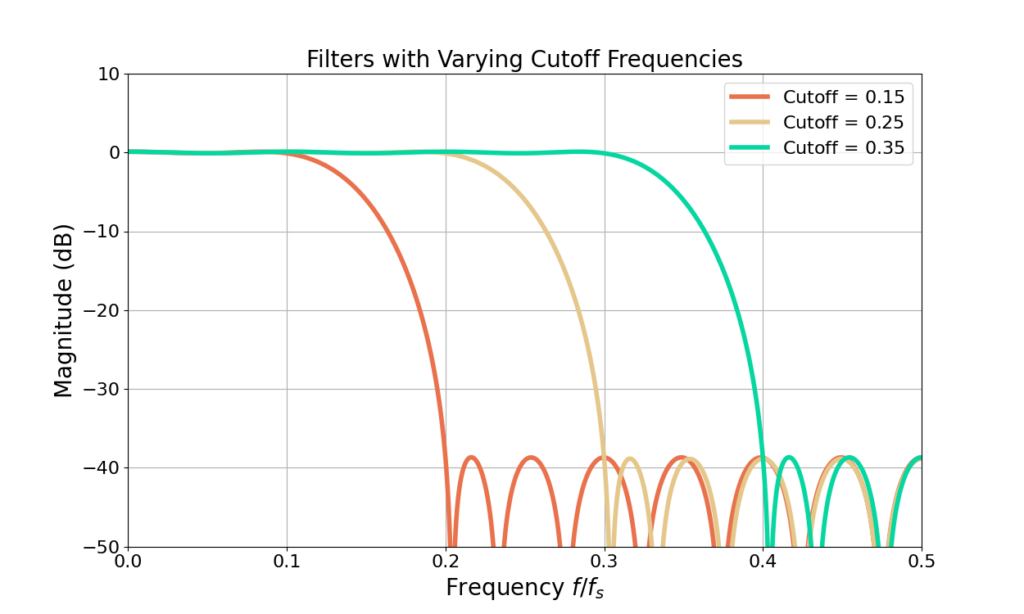
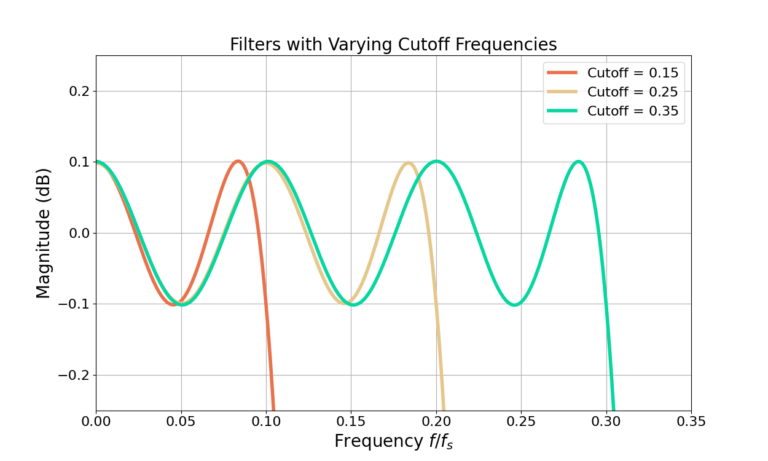
Figure 5 and Figure 6 shows changing the cut-off frequency changes the relative proportion of the pass-band and the stop-band of the filter but has no impact on either the pass-band ripple or stop-band attenuation.
However, holding the cut-off frequency constant and changing the transition bandwidth will impact the pass-band ripple and stop-band attenuation as seen in Figure 6 and Figure 7.
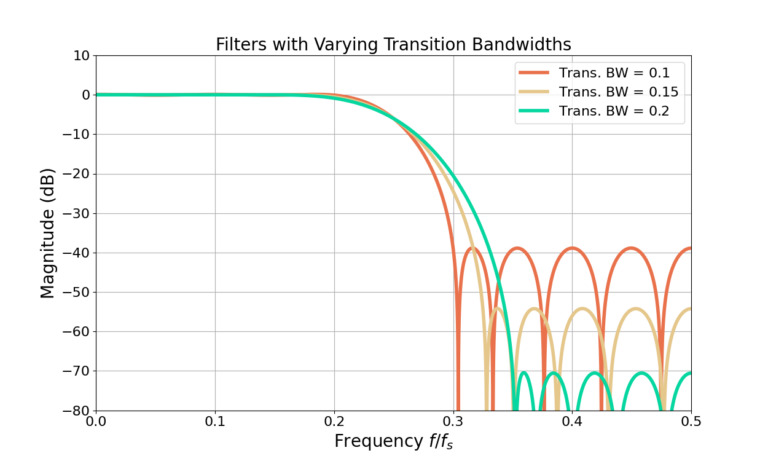
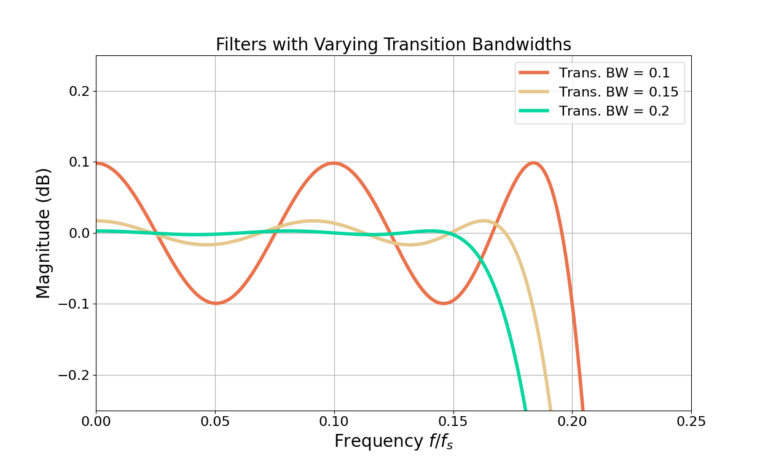
From Figure 7 and Figure 8 it can be seen that a larger transition bandwidth results in both smaller pass-band ripple as well as larger stop-band attenuation. Why?
Low Pass Filter Length Estimate
fred harris’ filter length approximation [harris2021, p.59] is
(2) ![]()
where ![]() is the transition bandwidth,
is the transition bandwidth, ![]() is the sampling frequency and
is the sampling frequency and ![]() is the sidelobe attenuation in dB. The frequencies
is the sidelobe attenuation in dB. The frequencies ![]() and
and ![]() can be in any units as long as they are consistent.
can be in any units as long as they are consistent.
The approximation in (2) shows that changes to the transition bandwidth will directly impact the sidelobe attenuation when the filter length is held constant. However the cut-off frequency has no impact which reinforces the earlier filters from Figures 4 – 8.
Using the parameters from Figure 7, ![]() =39 and
=39 and ![]() , the filter length for a transition bandwidth of
, the filter length for a transition bandwidth of ![]() is approximated to be
is approximated to be
(3) ![]()
Similarly from Figure 7, the second filter with ![]() and
and ![]() gives a filter length approximation of
gives a filter length approximation of
(4) ![]()
and the second filter with ![]() and
and ![]() gives a filter length approximation of
gives a filter length approximation of
(5) ![]()
The filter lengths are not exact but are reasonably close to the length L=21 the filter was designed with. It is typical for filter design to be an iterative “guess and check” process until the exact desired weights or frequency response is obtained.
Increasing Filter Length
More sidelobe attenuation can be obtained by increasing the filter length. Figure 9 and Figure 10 show the magnitudes of the frequency responses for filters with multiple lengths.
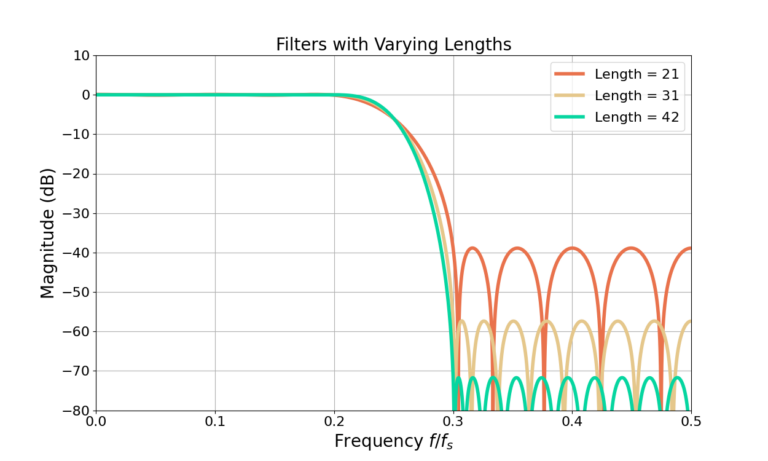
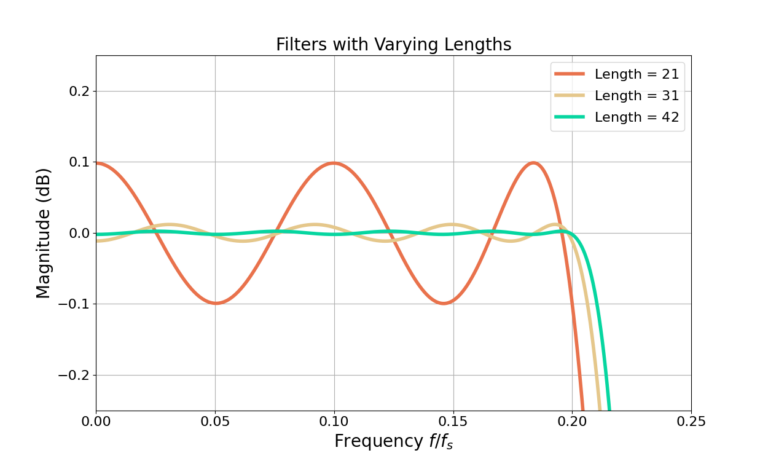
Trade-Offs
A great filter will have:
- a short length to reduce computation,
- a small transition band to maximize the amount of pass-band and stop-band,
- small pass-band ripple and large stop-band attenuation.
However, due to (2) a filter cannot have all three of these attributes and design trade-offs must be made. Figure 11 and Figure 12 show the example filter with L=21 and ![]() which has sidelobes at -39 dB and a pass-band ripple of 0.2 dB. The two other filters increase the sidelobe attenuation to about -70 dB by two different methods: doubling the transition bandwidth and doubling the filter length.
which has sidelobes at -39 dB and a pass-band ripple of 0.2 dB. The two other filters increase the sidelobe attenuation to about -70 dB by two different methods: doubling the transition bandwidth and doubling the filter length.
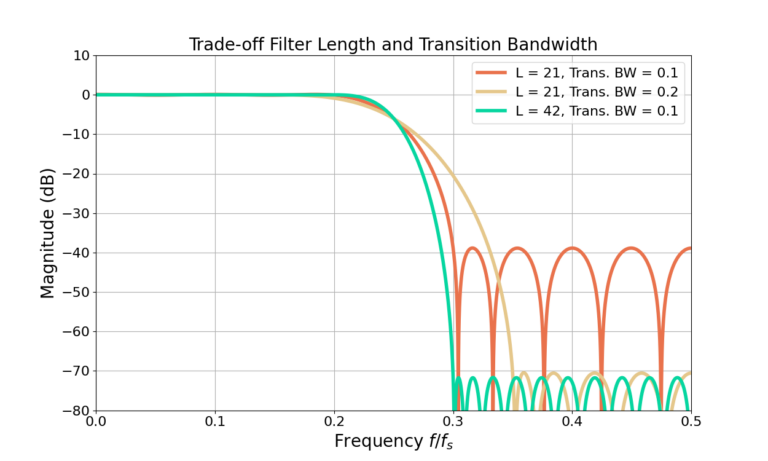
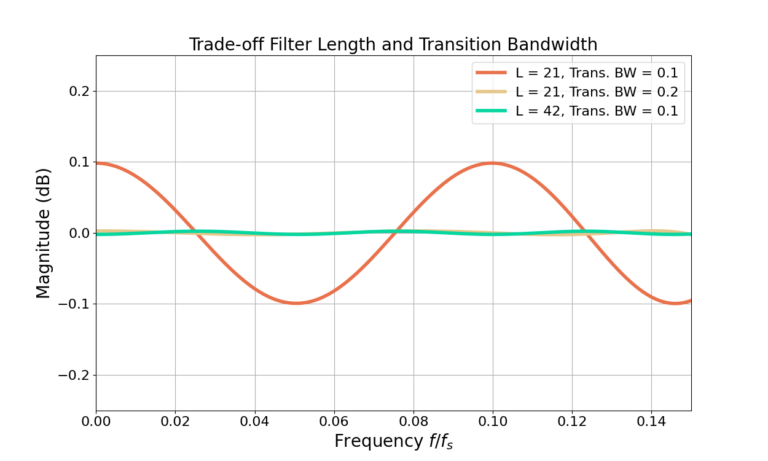
Increasing the filter length comes with the cost of more computation required to operate the filter which translates into:
- faster processor or FPGA,
- more heat,
- more cost,
- or lower system sampling rate.
Alternatively, increasing the transition bandwidth translates into:
a smaller pass-band,
a smaller stop-band,
and thus more undesired high-frequency content at the output of the filter.
Designing the filter weights requires balancing all of the different parameters in order to meet the specifications or application needs. For example some real-time applications may require a a smaller filter and can allow for worse sidelobes in order to operate at a high sampling rate, whereas other off-line applications can allow for longer filters to get the best possible sidelobe levels and small transition bandwidth.
Conclusion
Remez is a powerful tool for quickly designing FIR filter weights. A low-pass filter is designed by remez() by specifying the filter length, stop-band and pass-band frequencies as well as the amplitudes for the pass-band and stop-band. Alternatively, the cut-off frequency and transition bandwidth can be specified in the design. Increasing the transition bandwidth is an effective way for reducing the filter length or increasing the sidelobe attenuation. Similarly, a longer filter will require more computation but will have better attenuation or a smaller transition bandwidth. Trade-offs between all of the parameters will have to be made in order to make the best design that fits the application.
Be sure to check out these other posts on filter design!

![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x100.png)





