![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-75x75.png)
Table of Contents
Introduction
The square root raised cosine (SRRC) filter is used as a pulse shaping filter [harris2021, p.87] in many linear modulations such as BPSK, QPSK, and 16-QAM. Frustratingly neither SciPy or NumPy have a square-root raised cosine (SRRC) filter. Mathuranathan Viswanathan at GaussianWaves.com has a great post on how to build a square-root raised cosine filter. You can also find the design equations in [johnson2004, p.225, harris2021, p. 95].
I’ve written my own SRRC design script in Python which you can download from the WaveWalkerDSP GitHub page in the Blog Downloads repository.
Check out these other posts on filter design:
Example Square Root Raised Cosine Plots
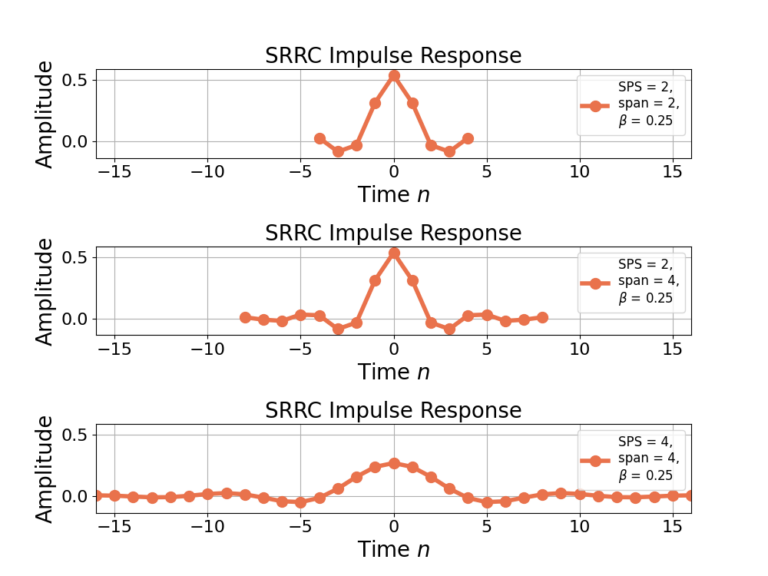
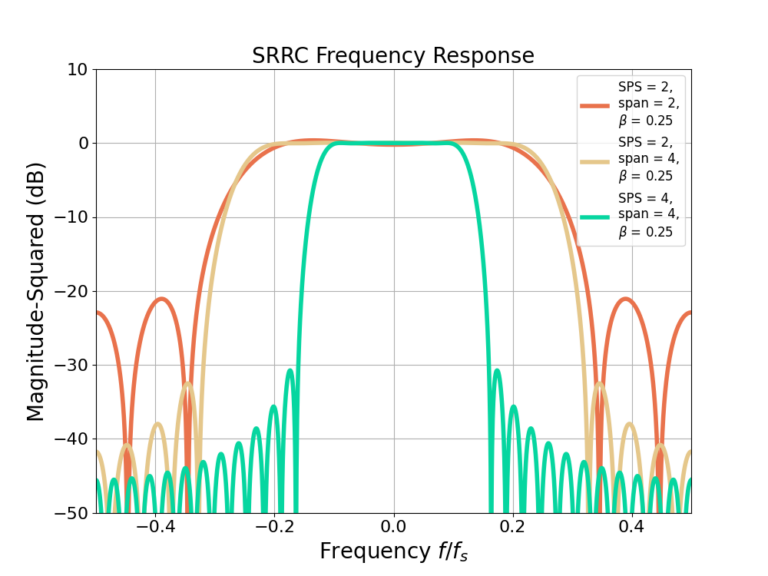
Figure 1 gives the impulse response for multiple SRRC filters with different SPS (samples per symbol), span (proxy for filter length) and 
(roll-off factor) values where Figure 2 gives the corresponding frequency response. The figures show that increasing the span for consistent SPS value reduces the sidelobes at the cost of a longer filter, however increasing the SPS reduces the cut-off frequency.
Conclusion
The srrcDesign.py file can be downloaded here.
Wondering about how and why the SPS, span and parameters effect the frequency response of the SRRC filters? Be sure to check out the post on low-pass filter design to understand the relationships between filter length, transition bandwidth and sidelobe attenuation.
Check out these other posts on filter design: