Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Designing an FIR Band Pass Filter with Remez

September 24, 2021

Introduction

A band pass filter is characterized by having attenuation at both high frequency and low frequency with a pass-band in between. Band-pass filters can designed to have real coefficients which have an even-symmetric response or they can be upconverted to complex band-pass to have non-symmetric response which is useful in channelization or in applying a Hilbert transform.

Additional examples for BPF Remez filter design can be found in the SciPy documentation.

Design a Real Band Pass Filter with Remez

An example pass-band filter can be designed with remez() by

import scipy.signal fCenter = 0.25 passbandWidth = 0.25 transBandBPF = 0.2 fPassLeft = fCenter - (passbandWidth/2) fPassRight = fCenter + (passbandWidth/2) fStopLeft = fPassLeft - (transBandBPF/2) fStopRight = fPassRight + (transBandBPF/2) fVec = [0, fStopLeft, fPassLeft, fPassRight, fStopRight, 0.5] aVec = [0, 1, 0] BPFRemez = scipy.signal.remez(filterLength,fVec,aVec)

Figure 1 displays the design parameters of the BPF and the desired shape of the magnitude of the frequency response, Figure 2 gives the actual frequency response in linear units. A BPF has two transition bands (Figure 1 and Figure 2), one to the left and one to the right of the passband. Therefore the transition bandwidth of 0.2 is divided to both, 0.1 to the left and 0.1 to the right.

Figure 3 gives the magnitude of the frequency response for the BPF in dB and Figure 4 displays the double sided spectrum from $-f_s/2$ to $f_s/2$ , or $-\pi$ to $\pi$ in radians.

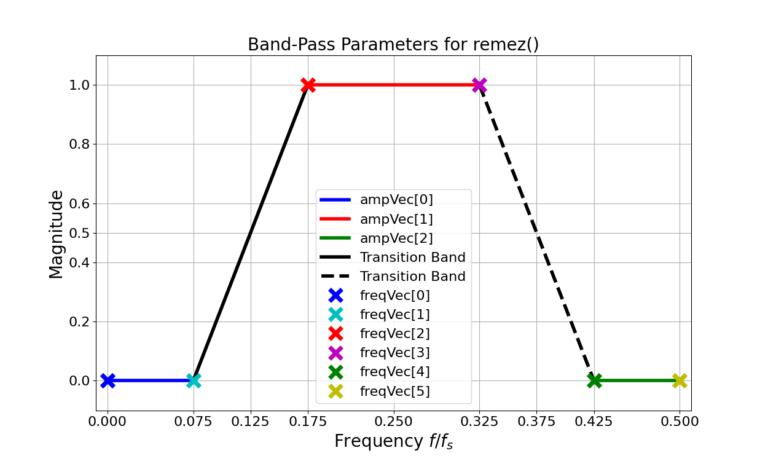
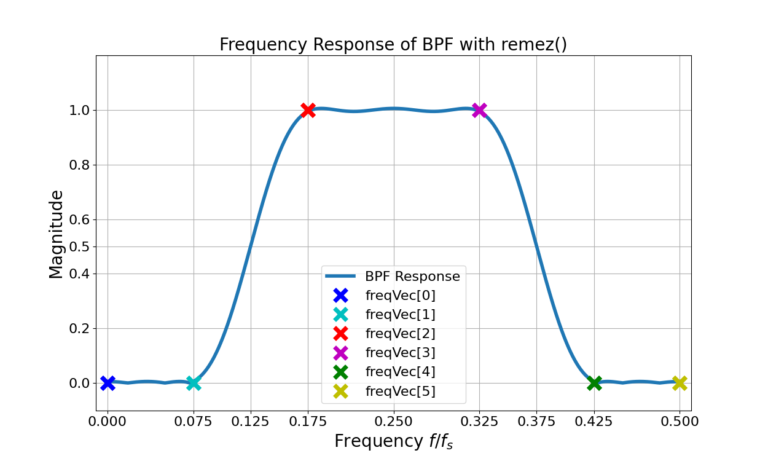
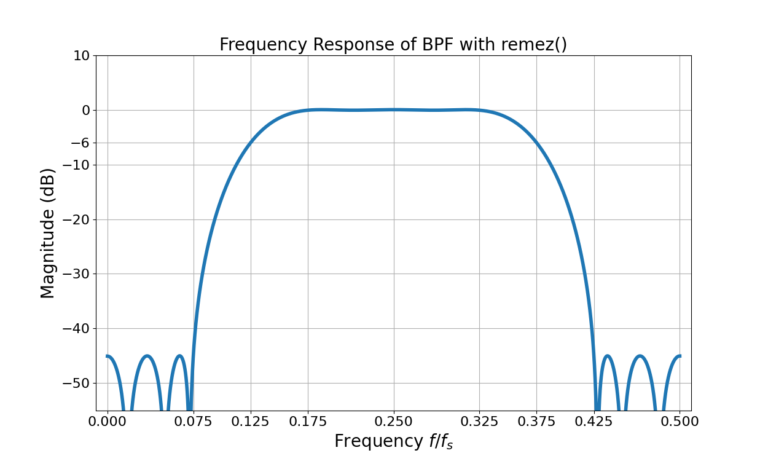
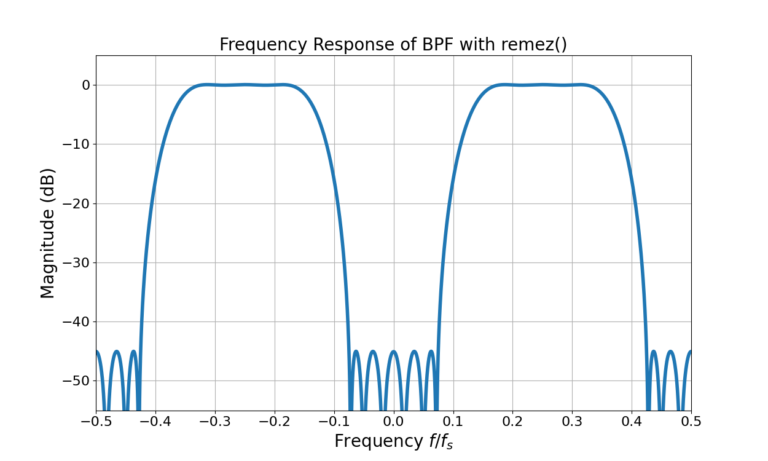
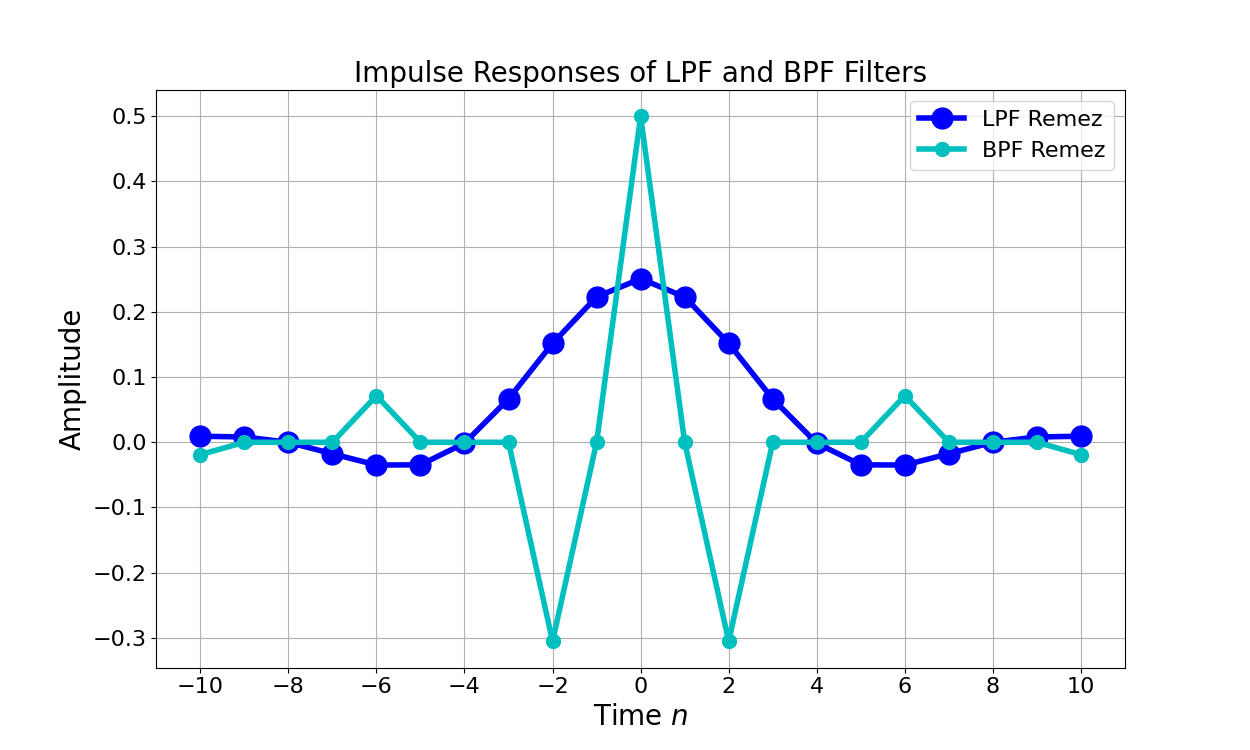
Figure 5 gives the impulse response for the Remez-designed LPF and BPF filters.

Problems with Upconverting a Low Pass Filter to a Real Band Pass Filter

Similar to the process from the high-pass filter design blog an LPF is designed and then upconverted to band-pass. The LPF is designed with

import scipy.signal filterLength = 21 cutoffLPF = 0.125 transBand = 0.1 fPassLPF = cutoffLPF - (transBand/2) fStopLPF = cutoffLPF + (transBand/2) fVec = [0, fPassLPF, fStopLPF, 0.5] aVec = [1, 0] LPFRemez = scipy.signal.remez(filterLength,fVec,aVec)

The filter weights are then upconverted to $f_s/4$ or $\pi/2$ in radians,

(1) $\begin{equation*}h_{BPF}[n] = h_{LPF}[n] \cdot cos(\pi n/2).\end{equation*}$

Figure 6 gives the frequency responses for the BPF designed with Remez as well as the LPF upconverted to band-pass.

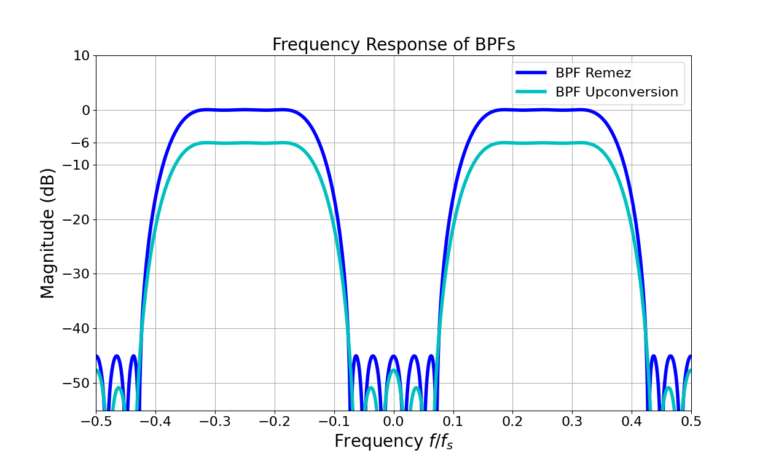
The first thing to note from Figure 6 is that the magnitude is 6 dB lower than the Remez version. Why?

Taking another look at the math, cosine can be expressed as the summation of two complex exponentials,

(2) $\begin{equation*}cos(\theta n) = \frac{1}{2} \left( e^{j\theta n} + e^{-j\theta n} \right).\end{equation*}$

Substituting (2) into (1),

(3) $\begin{equation*}\begin{split}h_{BPF}[n] & = h_{LPF}[n] \cdot \frac{1}{2} \left( e^{j\pi n/2} + e^{-j \pi n/2} \right) \\& = \left( \frac{1}{2} h_{LPF}[n] \cdot e^{j\pi n/2} \right ) + \left( \frac{1}{2} h_{LPF}[n] \cdot e^{-j\pi n/2} \right ).\end{split}\end{equation*}$

The LPF is turned into two copies at different frequencies whose magnitude is divided by 1/2. Scaling the upconverted BPF by 2 accounts for the relative loss compared to the Remez design,

(4) $\begin{equation*}h_{BPF}[n] = 2 \cdot h_{LPF}[n] \cdot cos(\pi n/2).\end{equation*}$

Figure 7 gives the frequency response for (4).

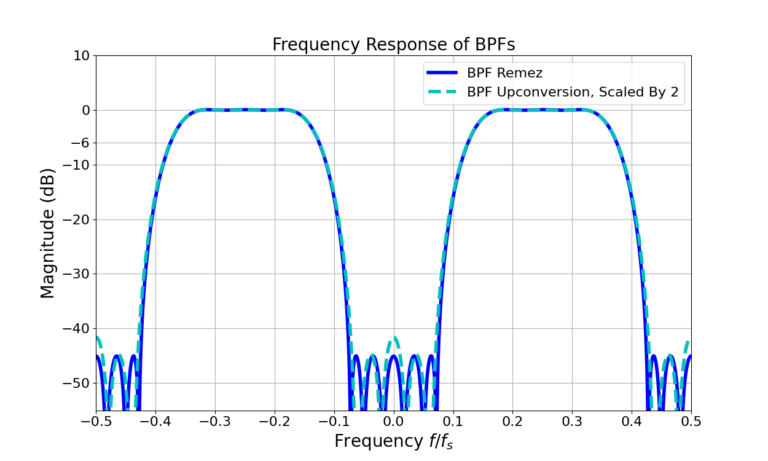
The scaling by 2 has matched the magnitude levels of the two filters in Figure 7 however the sidelobes now show a difference. The sidelobes are higher at $f/f_s = 0, -0.5, +0.5$ . Why?

The problem is $h_{LPF}[n] \cdot e^{j\pi n/2}$ and $h_{LPF}[n] \cdot e^{-j\pi n/2}$ interfere with one another in the frequency domain when they are summed. Figure 8 shows the two frequency responses of the complex upconversion to positive and negative frequencies of the BPF.

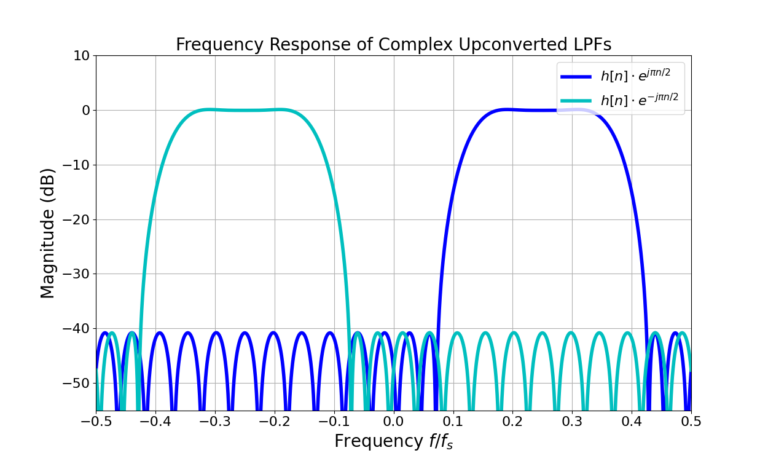
Due to the interference between the two copies of the filter it is better to design a BPF using Remez rather than attempt to build an LPF and upconvert it.

Upconvert Low-Pass to Complex Band-Pass

Real signals have an evenly symmetric magnitude [oppenheim1999, p.56], that is

(5) $\begin{equation*}|X\left( e^{j\omega} \right)| = |X \left( e^{-j\omega} \right) |.\end{equation*}$

Equation (5) is the reason why $h_{LPF}[n] \cdot cos(\pi n/2)$ has a passband in both the positive frequencies and negative frequencies. Such an even-symmetric respond may be acceptable when processing real signals but much of DSP is done at complex baseband and non-symmetric band-pass filters may be required in the case of channelizers, for selecting specific signals from a broad spectrum or applying a Hilbert transform [carrick2011].

Where $h_{BPF}[n]$ in (4) uses real upconversion complex upconversion can be used to translate a LPF into complex band-pass. Rather than use a cosine to perform the upconversion, a complex-exponential will allow the selection of one of the two BPF responses as in Figure 8.

The positive and negative frequency complex upconverted band-pass filter is given by

(6) $\begin{equation*}h_{+BPF}[n] = h_{LPF}[n] \cdot e^{j \phi n}\end{equation*}$

(7) $\begin{equation*}h_{-BPF}[n] = h_{LPF}[n] \cdot e^{-j \phi n}\end{equation*}$

where $\phi$ and \(-\phi)\ is the center frequency of the band-pass filter. The filters can be upconverted using the following code:

import numpy as np n = np.arange(-(filterLength-1)/2,(filterLength-1)/2+1) BPFPosUpconvert = LPFRemez*np.exp(1j*2*np.pi*n*(1/4)) BPFNegUpconvert = LPFRemez*np.exp(-1j*2*np.pi*n*(1/4))

The downside of the complex upconversion is that the filter weights are transformed from real to complex and therefore the filter now requires complex multiplication to implement it which requires more operations.

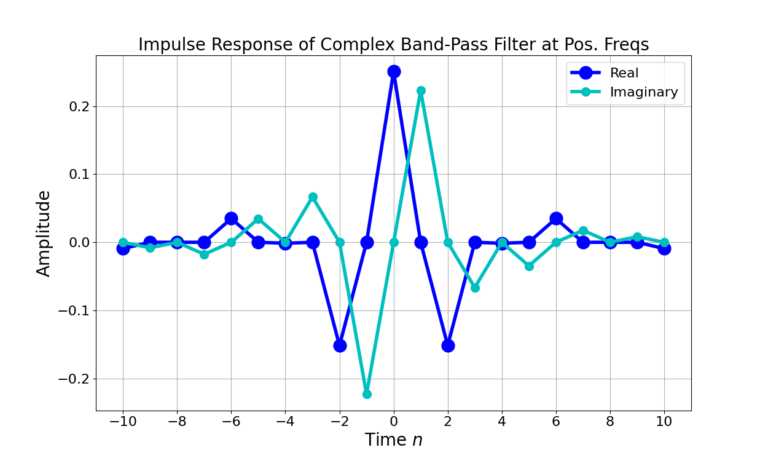
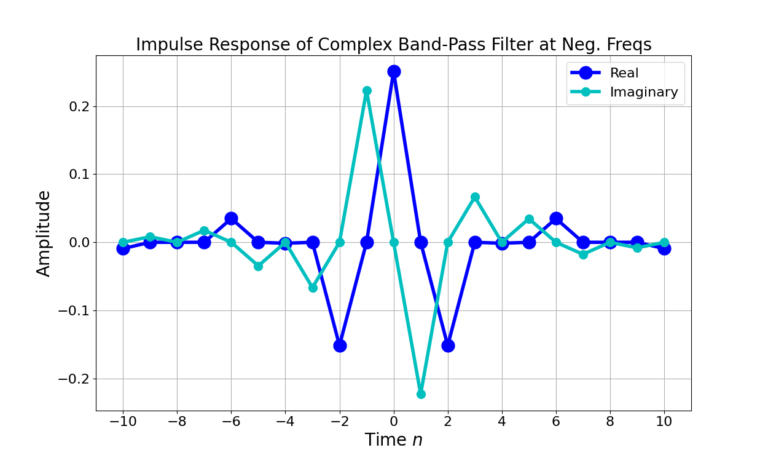
Figure 9 is the impulse response of the LPF being upconverted to complex pass-band at positive frequencies from (6) and Figure 10 is after being upconverted to negative frequencies from (7). Note that the imaginary portion of the impulse response is delayed with respect to the real for the positive frequency BPF in Figure 9. The real portion of the impulse response is delayed with respect to the imaginary in Figure 10 which is characteristic of a negative frequency sinusoid.

Conclusion

Real BPF filters are better designed with Remez rather than designing an LPF and upconverting it to pass-band due to the degradation in frequency response. However, designing a LPF and then performing a complex upconversion to complex pass-band creates the ability to have a non-symmetric frequency response which is useful in channelization and applying a Hilbert transform.

Don’t forget to check out these posts on filter design: