Table of Contents
Introduction
The goal of this post is to shed some light on why sinusoids are useful in DSP and RF communication.
Sinusoids are used by humans to describe the cyclical nature of the universe. They are a useful mathematical abstraction. Each year is 365 days and then a new year begins. Spring is followed by summer, fall, winter and then spring begins again. Low tide, high tide and then low tide again. A spinning ceiling fan. The rotation of the tires on your automobile. Reeling your fishing rod.
Check out these related blog posts:
Why Not?
I recall being an undergraduate student and thinking to myself:
Why is all of the math in DSP based around complex sinusoids?
The question you might try and answer for yourself is:
Why not?
What other mathematics might be a better substitute? Leave a comment below.
My intuition is that sinusoids are so inherent to our universe that it may be impossible or needlessly difficult to do DSP without them. Let’s take the scenic route in understanding the role of sinusoids in DSP and consider what role they play in another mode of communication: music.
Sinusoids in Music: The Xylophone
Did you realize that the xylophone you had as a child was actually an acoustic signal generator?
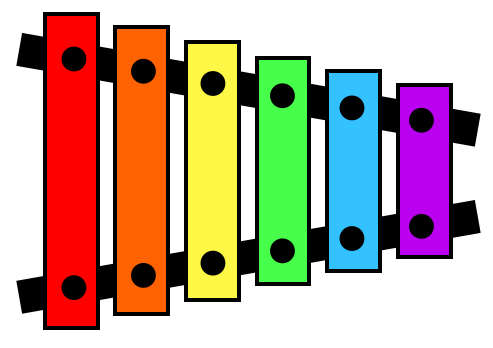
Striking the wooden mallet against one of the keys transforms the kinetic energy of the mallet into resonating the key. You’ll recall that that the different lengths of the keys in a xylophone correspond to different tones. You can watch a reminder video here. A longer key produces deeper sound where a shorter key produces a higher pitched sound.
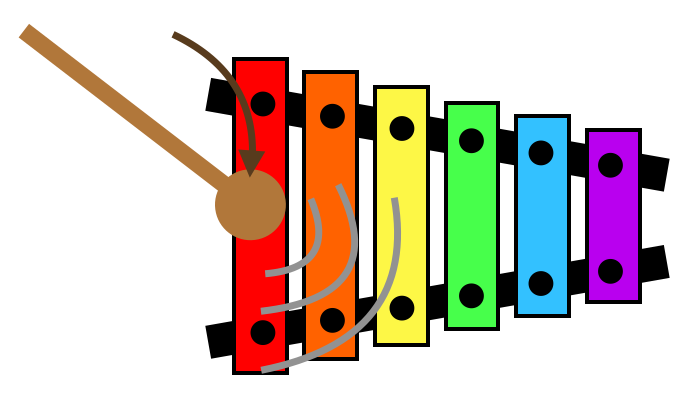
A standing wave is created based on the vibration of the metal key which in turn creates a pressure wave in the air which is the sound received by your ear. The length of the key directly relates to the frequency of the pressure wave and thus the tone you hear.
You’ll notice no sinusoids were forced onto the xylophone example: it was a physical property of the universe (harmonic resonance) that was described with sinusoids.
Before we move on from the xylophone, consider that you could create an acoustic communication method based on assigning bits to each of the keys and striking each key would then correspond to the transmission of the bits. This is the basic concept for frequency shift keying (FSK).
Sinusoids in DSP
In the same way that sinusoids are used to explain how acoustic waves create different pitched sounds, so too do sinusoids explain how electromagnetic waves convey information across the RF spectrum.
A voltage is impressed upon the length of an antenna which generates an electromagnetic wave. The frequency of the electromagnetic wave is related to the length of the antenna in the same way the length of the xylophone key is related to the frequency of the tone it generates. The electromagnetic wave then travels to a radio receiver designed for the specific transmission frequency.
In the same way the xylophone has a harmonic resonance which creates sound, so too does the antenna have a harmonic resonance that creates an electromagnetic wave.
Note again that the frequency of the electromagnetic wave is derived from its physical qualities and that sinusoids are simply used to explain or represent the phenomenon.
Conclusion
Many physical phenomenon are cyclical in nature. The frequency of electromagnetic waves comes from the properties of the antenna used in transmission. Sinusoids are a useful mathematical abstraction for representing the operation of physical systems which have a cyclical nature. Being able to speak the language of sinusoids is required for understanding how to design, analyze and implement DSP and RF systems.
Check out these other blogs!
![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x100.png)







3 Responses
Good question, especially for EE/DSP students, and a good example of the *kinds* of questions we need to ask students, and lead them to ask themselves.
My own answers predictably bend toward the mathematical. A sine wave is the ‘eigenfunction’ of a linear time-invariant system, more commonly referred to as a filter, which simply means if you use a sine wave with frequency F as an input, you get a sine wave with frequency F as an output, and nothing else. The filter changes the magnitude and phase (delay) of the sine wave, but does not create new sine waves. And we care very much about linear time-invariant systems because they are observed in the world (at least to a good approximation) and they are very useful (as you point out elsewhere) for modifying the properties of signals.
The second reason for our enduring preoccupation with sine waves is the Fourier series. Any periodic function can be represented (with some mathematical caveats that aren’t too important to a practicing DSP engineer) as a sum of weighted harmonically related sine waves. And periodic (non-sinusoidal) functions form the basis for communication signals, such as modulated pulse trains. And of course the Fourier series leads directly to the Fourier transform, the most powerful tool in our signal processing toolkit (my opinion of course).
My $0.02.
Thanks for a thought-provoking post. Looking forward to more in this category!
Thank you Chad! I agree 100%.
Chad’s blog cyclostationary.blog is excellent and something I read frequently. It’s worth while reading through his post on the Fourier series https://cyclostationary.blog/2020/03/08/sptk-the-fourier-series/.