Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Phase, Frequency and Negative Frequency in Complex Sinusoids

October 19, 2021

Introduction

A prior post described how sinusoids came to be used in DSP and RF due to physical properties of the universe. A follow up gave some mathematical rules about complex sinusoids on how sine, cosine and $e^{j\phi}$ all related to one another in terms of Euler’s triangle. This blog will continue by including time in complex sinusoids, describe how phase and frequency relate to one another, how a negative frequency arises and demonstrates the concepts using the unit circle. It may be useful to review some complex math before jumping into this post.

Additional blog posts on complex numbers:

Instantaneous Phase

Euler’s formula

(1) $\begin{equation*}e^{j \phi} = cos(\phi) + j \cdot sin (\phi)\end{equation*}$

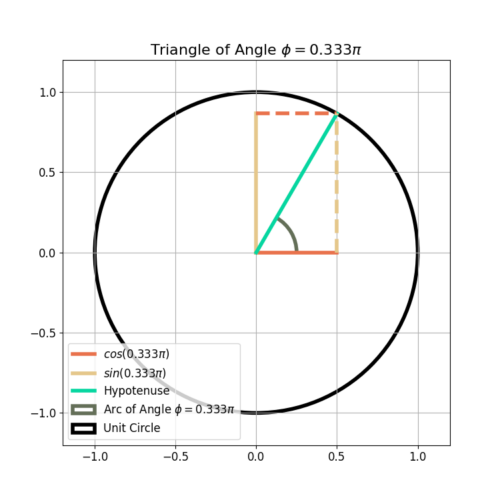
is used to describe the position of a vector on the unit circle in the complex plane as shown in Figure 1.

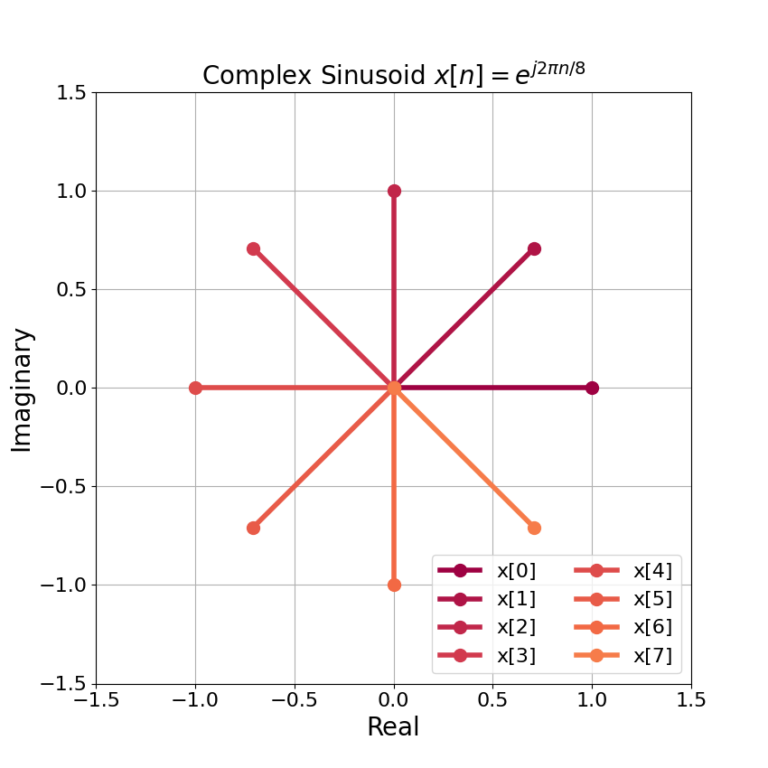
Similarly Euler’s formula can be given as

(2) $\begin{equation*}e^{j \omega n} = \text{cos}(\omega n) + j\cdot \text{sin}(\omega n)\end{equation*}$

which describes a complex sinusoid rotating around the unit circle with time n. An example of a complex sinusoid $e^{j 2\pi n/8}$ is given in Figure 2. The complex sinusoid can be created in Python by

import numpy as np n = np.arange(0,8) complexSinusoid = np.exp(2j*np.pi*n/8)

The instantaneous phase of a complex sinusoid is the angle from 0 radians in the complex plane at some time n. For

(3) $\begin{equation*}x[n] = e^{j\omega n}\end{equation*}$

the instantaneous phase is given by

(4) $\begin{equation*}\sphericalangle{x[n]} = \sphericalangle{e^{j\omega n}} = \omega n.\end{equation*}$

As the complex sinusoid rotates through the unit circle the instantaneous phase will change with time n. From the example in Figure 2 the complex sinusoid is $e^{j 2\pi n /8}$ such that the instantaneous phase is

(5) $\begin{equation*}\sphericalangle{e^{j2\pi n/8}} = 2\pi n/8.\end{equation*}$

From (5), the instantaneous phase is

(6) $\begin{equation*}\begin{split}\sphericalangle{x[0]} & = e^{j 0} = 0, \\\sphericalangle{x[1]} & = e^{j 2\pi/8} = 2\pi/8 = pi/4, \\\sphericalangle{x[2]} & = e^{j 4\pi/8} = 4\pi/8 = \pi/2 \\\end{split}\end{equation*}$

which can be seen in Figure 2.

Instantaneous Frequency

Where the instantaneous phase is the phase of a complex sinusoid at time n the instantaneous frequency is the velocity at which the complex sinusoid is rotating through the unit circle at time n.

From the example complex sinusoid $e^{j 2\pi n/8}$ in Figure 2 the instantaneous phase moves by $2\pi/8$ for each time n. The frequency in this case is therefore $2\pi/8$ because it describes the velocity at which the complex sinusoid is rotating through the unit circle.

It can also be stated that the instantaneous frequency is the time-derivative of the instantaneous phase

(7) $\begin{equation*}\begin{split}\frac{d}{dn} \sphericalangle{x[n]} & = \frac{d}{dn} \sphericalangle{e^{j \omega n}} \\& = \frac{d}{dn} \omega n \\& = \omega,\end{split}\end{equation*}$

or the instantaneous phase is the integral of the instantaneous frequency

(8) $\begin{equation*}\sphericalangle{x[n]} = \sum_{k=0}^{n-1} \omega = \omega n.\end{equation*}$

Figure 3 gives an example of the instantaneous phase for $e^{j2\pi n/8}$ . The unwrapped phase is (8) which has unbounded phase values and the wrapped phase applies the modulo operator to keep all values within $[-\pi, \pi]$ . Note that the instantaneous frequency is the derivative of the unwrapped phase which is $2\pi/8$ in this case. The instantaneous phase can be calculated from the sinusoid by

instPhase = np.angle(complexSinusoid)

and wrapping the phase by

instPhaseUnwrap = np.unwrap(instPhase)

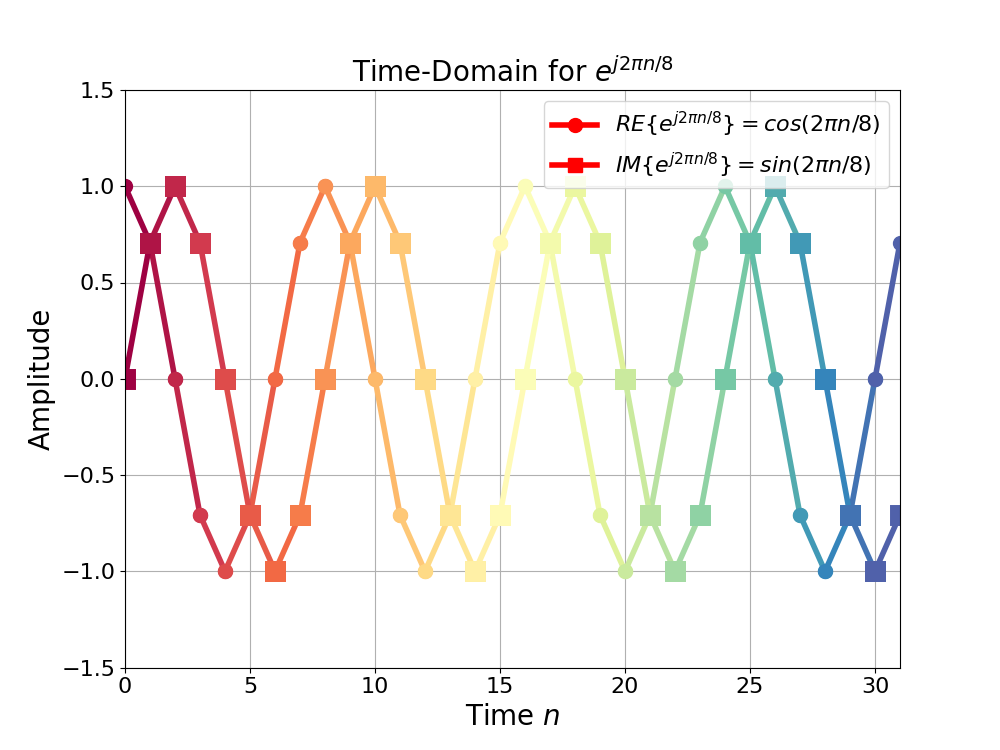
Figure 4 is the time-domain plot for $e^{j2\pi n/8}$ .

Negative Frequency

The trap in thinking about frequency is that it represents how often something happens, which is tricky because it is partially true. An incomplete definition of frequency would be how quickly a complex sinusoid rotates through the unit circle. The correct way to think about frequency it is is the speed and direction a complex sinusoid is rotating around the unit circle.

The complex sinusoid $e^{j2\pi n/8}$ has an instantaneous frequency of $2\pi/8$ which is the speed of the rotation around the unit circle in a counter-clockwise direction as in Figure 2. The complex sinusoid $e^{-j2 \pi n/8}$ has an instantaneous frequency of $-2\pi/8$ which is the speed of rotation the unit circle in a clockwise direction as in Figure 5.

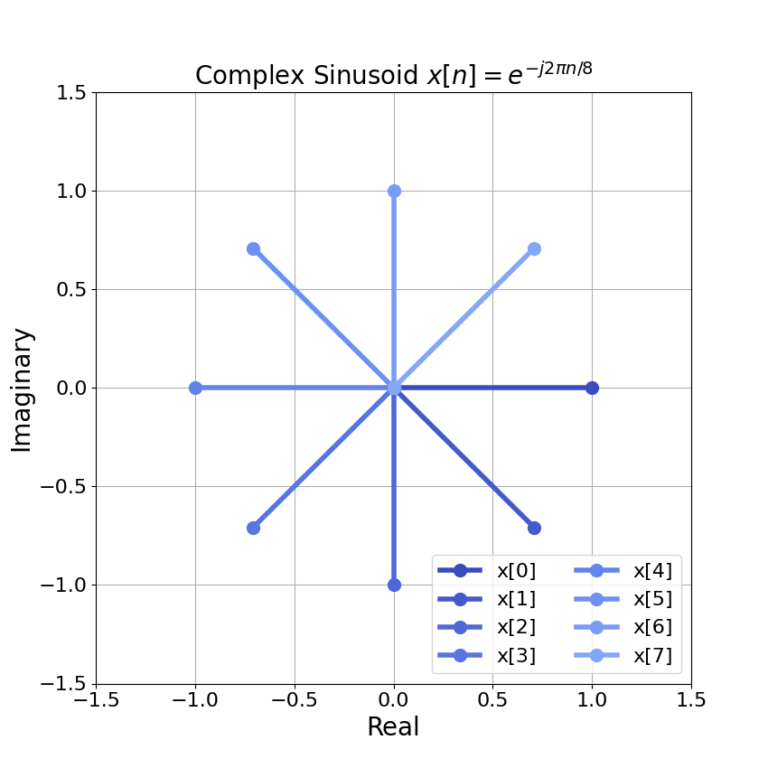
Figure 6 is a plot of the instantaneous phase for $e^{-j2\pi n/8}$ which shows a negative slope of the unwrapped phase, $-2\pi/8$ , because the frequency is negative. Compare against the positive slope in Figure 3.

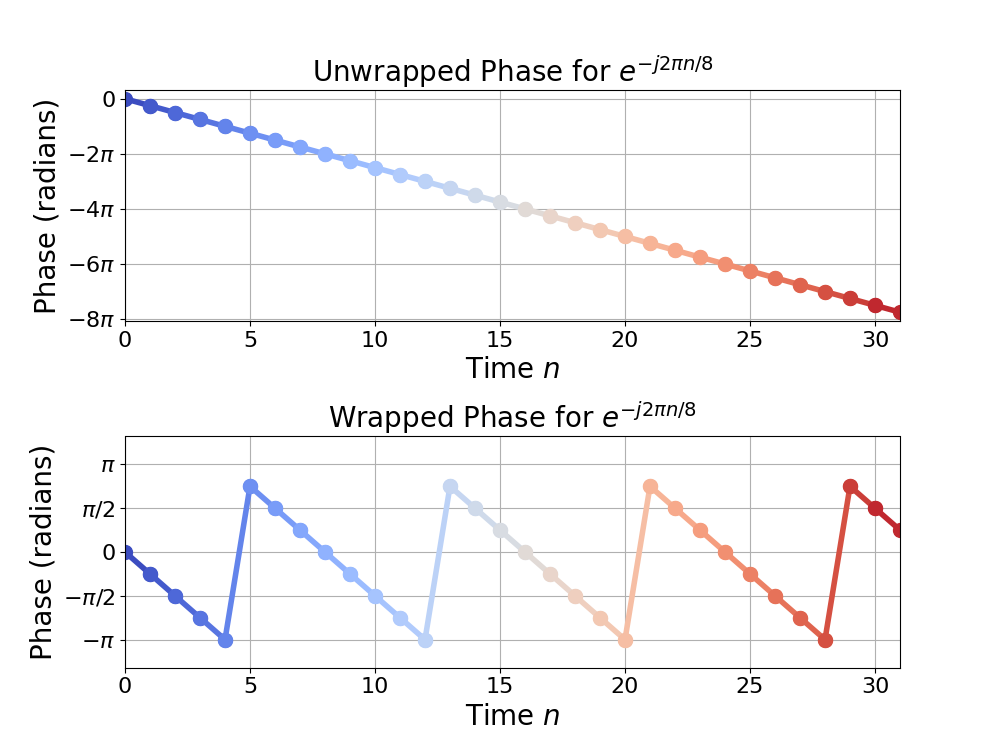
Figure 7 gives a time-domain plot for $e^{-j 2\pi n/8}$ which shows that a negative frequency changes the phase relationship between the $\cos(\cdot)$ and $\sin(\cdot)$ elements as compared to Figure 4. Where the real element $\cos(\cdot)$ leads the imaginary element $\sin(\cdot)$ for a positive frequency complex sinusoid, the reverse is true for a negative frequency complex sinusoid.

Phase Offset

It’s important to draw the distinction between instantaneous phase and phase offset since the two are related but differ. For a complex vector

(9) $\begin{equation*}e^{j(\omega n + \theta)}\end{equation*}$

the instantaneous phase is the angle at time n,

(10) $\begin{equation*}\sphericalangle{e^{j(\omega n + \theta)}} = \omega n + \theta\end{equation*}$

where the phase offset is $\theta$ . The phase offset can be summarized as the instantaneous phase at time n=0.

Conclusion

The instantaneous phase and frequency of a complex sinusoid are directly related to one another and understanding the relationship is important before moving onto more sophisticated DSP algorithms. The relationship can be summarized as the instantaneous phase is the integral of the instantaneous frequency and the instantaneous frequency is the derivative of the instantaneous phase.

A complex sinusoid can have a positive or negative frequency. A positive frequency is rotation around the unit circle in a counter-clockwise direction where as a negative frequency is rotation in a clockwise direction. Additionally, a positive frequency complex sinusoid will have the real element lead the imaginary element in the time domain, but the reverse is true for a negative frequency complex sinusoid.

Don’t forget to check out these other blog posts on complex numbers!