Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

How Euler’s Formula Relates Triangles, the Unit Circle and Complex Sinusoids

September 16, 2021

Introduction

Sines and cosines are the foundation for representing signals and the affects of filters and therefore understanding their mathematics is one of the foundational tools for signal processing. Euler’s formula is a mathematically compact and useful representation used for representing complex sinusoids.

Sine and Cosine

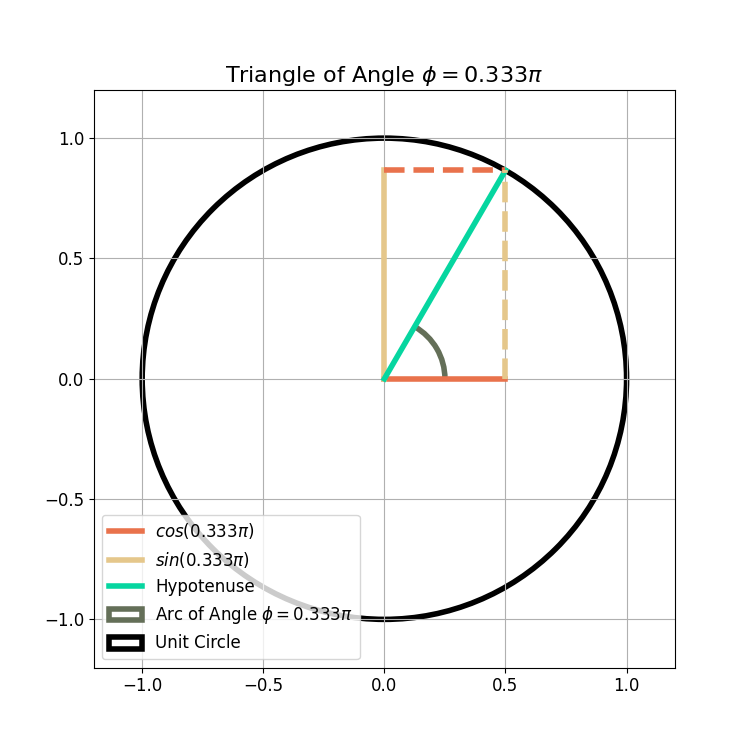
Sine and cosine refer to the opposite and adjacent lengths of a triangle with angle $\phi$ as shown in Figure 1.

Sine, referenced as $\sin(x)$ , is a perfectly periodic function in x where

(1) $\begin{equation*}\text{sin}(x) = \text{sin}(x + 2\pi)\end{equation*}$

for any x. The lengths of the triangle in Figure 1 will continually repeat as $\phi$ cycles from 0 to $2\pi$ , then $2\pi$ to $4\pi$ , and so on.

Sine and cosine are just phase shifts of one another, such that

(2) $\begin{equation*}\text{sin}\left(x + \frac{\pi}{2}\right) = \text{cos}(x),\end{equation*}$

(3) $\begin{equation*}\text{sin}(x) = \text{cos}\left(x - \frac{\pi}{2}\right).\end{equation*}$

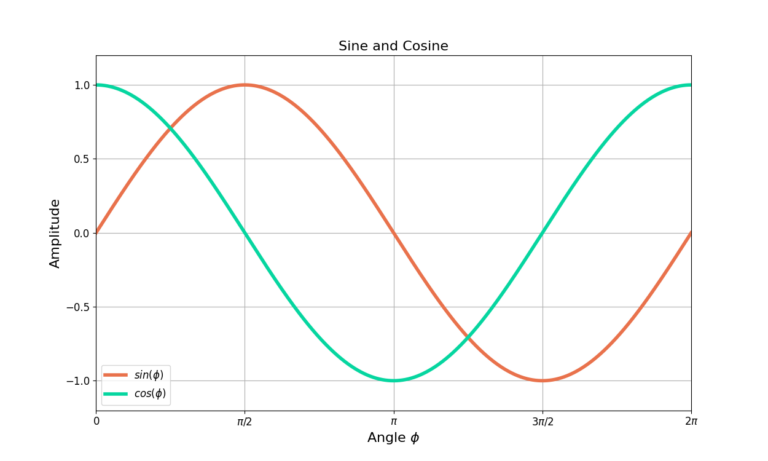
Figure 2 gives an example of $\sin(\phi)$ and $\cos(\phi)$ . Notice that sine and cosine are linked together as $\phi$ travels around the unit circle, the only difference being that cosine lags sine by $\pi/2$ .

Sine Wave

Where the terms sine and cosine refer to a single angle, a sine wave or sinusoid refers to $\sin(x)$ and $\cos(x)$ which vary over multiple values of x. To be useful as a mathematical tool a sine wave will have three parameters which describe it completely: amplitude A, frequency $\omega$ and phase $\theta$ ,

(4) $\begin{equation*}A ~ \text{sin}( \omega t + \theta)\end{equation*}$

where t is time. Figure 3 gives examples of how a sine wave is effected by different values of A, $\omega$ and $\theta$ .

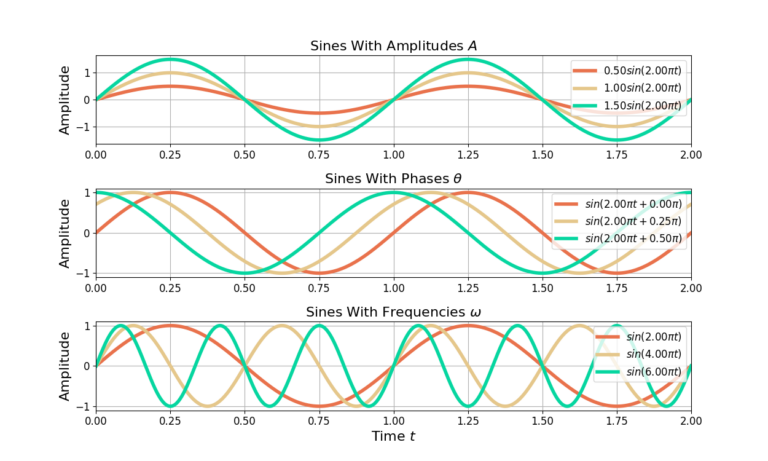
The amplitude A changes the vertical scale of the sinusoid and is related to the energy of the sine wave.

The phase $\theta$ relates to the position the sinusoid starts. For example, $\theta = 0$ refers to the angle of the triangle as if it was a clock hand pointing at 3 o’clock. The phase $\theta$ also can appear as a time delay as larger values seem to time-shift the sinusoid.

The frequency $\omega$ refers to the speed and direction at which the triangle’s angle is rotating from 0 to $2\pi$ . A positive frequency means the angle will cycle through the unit circle in a counter-clockwise direction where as a negative frequency will have the angle cycle through the unit circle in a clockwise direction. A larger frequency means the angle will cycle through the unit circle faster than a small frequency in the same measure of time.

Euler's Formula

Leonhard Euler (pronounced oiler) created the formula which relates sine and cosine through a complex exponential $e^{j\phi}$ according to

(5) $\begin{equation*}e^{j\phi} = \text{cos}(\phi) + j\cdot\text{sin}(\phi)\end{equation*}$

where $j = \sqrt{-1}$ . The complex sinusoid can be described more generically as of the form in (4) by

(6) $\begin{equation*}Ae^{j\left(\omega t + \theta\right)} = A\text{cos}(\omega t + \theta) + j\cdot\text{sin}(\omega t + \theta),\end{equation*}$

with amplitude A, frequency $\omega$ and phase $\theta$ .

Euler’s formula is a mathematically compact tool for representing sinusoids. A complex sinusoid simultaneously represents both the real $cos()$ and imaginary $sin()$ portion. The real portion can be obtained by using the real $\text{RE}\{\cdot\}$ operator and the imaginary portion can be selected by using the imaginary $\text{IM}\{\cdot\}$ operator such that

(7) $\begin{equation*}\text{RE}\left\{ Ae^{j\left( \omega t + \theta \right)} \right\} = A cos ( \omega t + \theta),\end{equation*}$

(8) $\begin{equation*}\text{IM}\left\{ Ae^{j\left( \omega t + \theta \right)} \right\} = A sin ( \omega t + \theta).\end{equation*}$

Additional Relationships

Two other mathematical properties are useful which relate $\cos()$ and $\sin()$ individually to complex exponentials are

(9) $\begin{equation*}cos(x) = \frac{1}{2} \left( e^{jx} + e^{-jx} \right),\end{equation*}$

(10) $\begin{equation*}sin(x) = \frac{1}{2j} \left( e^{jx} - e^{-jx} \right).\end{equation*}$

Equation (9) can be derived from (5) by adding $e^{-j\phi}$ ,

(11) $\begin{equation*}\begin{split}e^{j\phi} + e^{-j\phi} & = \left( \text{cos}(\phi) + j\cdot\text{sin}(\phi)\right) + \left( \text{cos}(\phi) - j\cdot\text{sin}(\phi)\right) \\& = 2 \text{cos}(\phi).\end{split}\end{equation*}$

Dividing both sides of (11) by 2 gives the final relationship,

(12) $\begin{equation*}\frac{1}{2} \left( e^{j\phi} + e^{-j\phi} \right) = \text{cos}(\phi).\end{equation*}$

Similarly (10) can be derived from (5) by subtracting $e^{-j\phi}$ ,

(13) $\begin{equation*}\begin{split}e^{j\phi} - e^{-j\phi} & = \left( \text{cos}(\phi) + j\cdot\text{sin}(\phi)\right) - \left( \text{cos}(\phi) - j\cdot\text{sin}(\phi)\right) \\& = 2j \cdot \text{sin}(\phi).\end{split}\end{equation*}$

Dividing both sides of (13) by 2j gives the final relationship,

(14) $\begin{equation*}\frac{1}{2j} \left( e^{j\phi} - e^{-j\phi} \right) = \text{sin}(\phi).\end{equation*}$

Conclusion

Sines and cosines are a foundational tool in DSP. Understanding the phase relationships between sine and cosine, as well as Euler’s formula (5) and its representations (9) and (10) are foundational to understanding before building more sophisticated DSP algorithms.

Don’t forget to check out these blogs on complex sinusoids:

One Response

Pingback: can a triangle have a 0 degree angle? – What Type Degree