Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

The Unit Circle: The Field of Play for the Game of DSP

October 23, 2021

Introduction

Thinking about complex sinusoids, $\sqrt{-1} = j$ , the unit circle, phase, negative frequency and using $\pi$ instead of $180^\circ$ can all be confusing when the material is first encountered. Have you asked yourself the following questions? I certainly have:

Why do we need the complex plane?
Why can’t we just use degrees instead of radians?
Why is the unit circle useful?

Unfortunately many of the mathematical tools encountered in the first and second years of an undergraduate EE degree are abstract and their value may not seem practical until graduate school or your first job as an engineer. The hope is that the following post will connect these concepts into a real world situation using the face of a clock in an attempt to build some intuition.

Additional blog posts on complex numbers:

The Unit Circle

The unit circle is a foundational concept and is used as the reference geometry in all of DSP. Baseball has to have the baseball field with its foul lines, outfield fence and base paths which are the foundation for all other rules in the game. Driving from one city to another requires foundational geometry: north, south, east and west. So too does DSP need its foundational geometry, the unit circle.

The unit circle is field the game of DSP is played upon. The unit circle is the reference allowing the measurement of parameters such as phase and frequency. The unit circle is used to create modulations for transmitters and compute center frequency offset for receivers.

The unit circle is a circle of radius 1 within the complex plane. The unit circle can be thought of as a complex vector $e^{j \phi}$ with unit magnitude $|e^{j\phi}| = 1$ being swept across all values of $\phi = [-\pi, \pi]$ . The angle from 0 radians or $0^\circ$ is given by $\sphericalangle{ e^{j \phi} } = \phi$ .

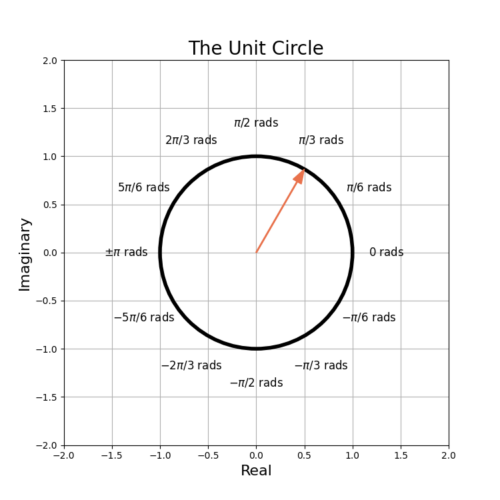
By convention the angles of the unit circle are given in radians, most commonly from $-\pi$ to $\pi$ or sometimes from 0 to $2\pi$ . Figure 1 shows the unit circle with an example complex vector $e^{j\pi/3}$ whose phase is $\pi/3$ as labeled on the plot.

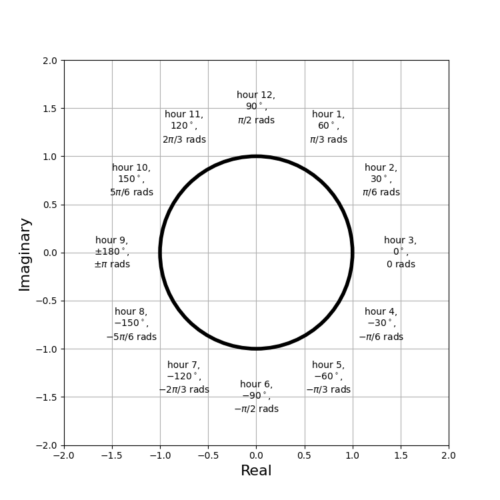
Angles on Face of Clock

Figure 2 overlays the unit circle and the angles onto the face of a clock.

The hours and their corresponding phase angle on the unit circle are given by

(1) $\begin{equation*}\begin{split}\text{hour} ~ 12, & ~ \text{phase} ~ 90^\circ, \pi/2 ~\text{radians}, \\\text{hour} ~ 1, & ~ \text{phase} ~ 60^\circ, \pi/3 ~\text{radians}, \\\text{hour} ~ 2, & ~ \text{phase} ~ 30^\circ, \pi/6 ~\text{radians}, \\\text{hour} ~ 3, & ~ \text{phase} ~ 0^\circ ~ \text{or} ~ 360^\circ, 0 ~ \text{or} ~ 2\pi ~\text{radians}, \\\text{hour} ~ 4, & ~ \text{phase} ~ -30^\circ, -\pi/6 ~\text{radians}, \\\text{hour} ~ 5, & ~ \text{phase} ~ -60^\circ, -\pi/3 ~\text{radians}, \\\text{hour} ~ 6, & ~ \text{phase} ~ -90^\circ, -\pi/2 ~\text{radians}, \\\text{hour} ~ 7, & ~ \text{phase} ~ -120^\circ, -2\pi/3 ~\text{radians}, \\\text{hour} ~ 8, & ~ \text{phase} ~ -150^\circ, -5\pi/6 ~\text{radians}, \\\text{hour} ~ 9, & ~ \text{phase} ~ \pm 180^\circ, \pm \pi ~\text{radians}, \\\text{hour} ~ 10, & ~ \text{phase} ~ 150^\circ, 5\pi/6 ~\text{radians}, \\\text{hour} ~ 11, & ~ \text{phase} ~ 120^\circ, 2\pi/3 ~\text{radians}. \\\end{split}\end{equation*}$

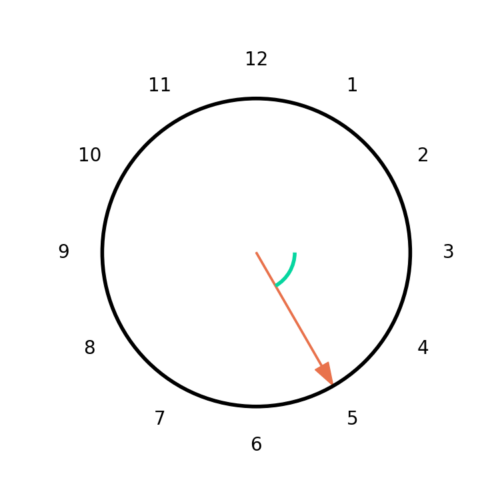
Instantaneous Phase

The instantaneous phase is the angle of the complex vector measured from 0 radians at a given time. For the face of a clock the instantaneous phase is the angle from 3 o’clock at a given moment. For simplicity the clock will only use hours and the minute and second hands will be ignored.

Figure 3 gives an example of the clock hand pointing to 5 o’clock. From Figure 1 and (1) 5 o’clock on the face of the clock is an instantaneous phase of $-\pi/3$ .

Instantaneous Frequency

Instantaneous frequency is the velocity at which a complex sinusoid is rotating around the unit circle. Where phase is give in radians frequency is given in radians per second. By analogy the instantaneous frequency $\omega_{clock}$ is the velocity of the clock hand rotation around the face of the clock. Recall that the instantaneous frequency $\omega$ is the time-derivative of the instantaneous phase $\phi$

(2) $\begin{equation*}\omega = \frac{\Delta \phi}{\Delta t}.\end{equation*}$

The clock hand moves at a constant speed so the time-derivative can be calculated by

(3) $\begin{equation*}\omega = \frac{\phi_{1} - \phi_{0}}{\Delta t}.\end{equation*}$

Figure 4 shows an example where the clock hand has moved from 8 to 12.

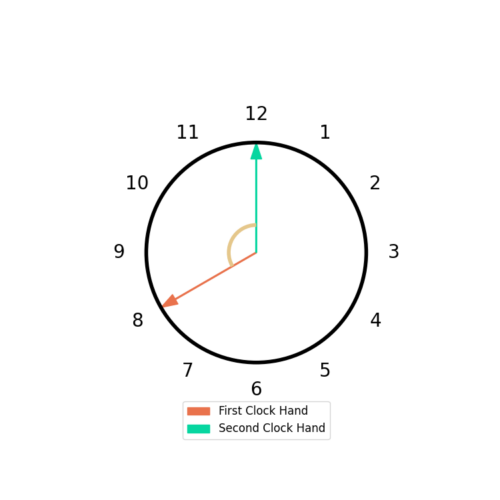
From (1) the phase at hour 8 is $\phi_{0}=-5\pi/6$ and the phase at hour 12 is $\phi_{1} = \pi/2$ . The angle $\phi_{0}=-5\pi/6$ is converted into a positive angle

(4) $\begin{equation*}\phi_{0} = -5\pi/6 + 2\pi = 7\pi/6,\end{equation*}$

so the subtraction $\phi_{1} - \phi_{0}$ is not done across the $\pm \pi$ boundary. The change in phase is therefore

(5) $\begin{equation*}\phi_{1} - \phi_{0} = \pi/2 - 7\pi/6 = -2\pi/3\end{equation*}$

and the change in time is

(6) $\begin{equation*}\Delta t = 4 ~ \text{hours}.\end{equation*}$

From Figure 4 and (5) and (6) the frequency is

(7) $\begin{equation*}\omega = \frac{-2\pi/3}{4} = -\frac{\pi}{6} ~ \frac{\text{radians}}{\text{hour}}.\end{equation*}$

By convention negative frequencies rotate in counter-clockwise direction and (7) is consistent with this. After converting to degrees the frequency is

(8) $\begin{equation*}\omega \cdot \frac{180}{\pi} = - \frac{\pi}{6} \cdot \frac{180}{\pi} = -30^{\circ} ~ \text{per hour}}\end{equation*}$

which is correct because the face of the clock has $360^\circ$ and is divided into 12 hours thus allocating each hour $360^\circ / 12 = 30^\circ$ . Normalized frequencies are typically given in radians/second and therefore the frequency is

(9) $\begin{equation*}\frac{\pi}{6} \cdot \frac{1}{3600} = \frac{1}{21600} \frac{\text{radians}}{\text{second}}\end{equation*}$

(10) $\begin{equation*}30^{\circ} \cdot \frac{1}{3600} = \frac{1}{120} \frac{\text{degrees}}{\text{second}}.\end{equation*}$

Conclusion

There is a word to describe people who are confused by the mathematics of DSP: normal.

Remember:

The instantaneous phase of a complex vector can be thought of as the angle from 3 o’clock.
The instantaneous frequency can be thought of as the velocity at which the clock hand is rotating over the face of the clock.
The unit circle is like the outline on the face of the clock where the hours are labeled.
The unit circle is the field upon which the game of DSP is played.

The goal of this post was to connect abstract concepts into a real world scenario in an attempt to build some intuition about phase, frequency and the unit circle. Hopefully posts such as Phase, Frequency and Negative Frequency and Basic Rules for Complex Math are easier to understanding after reading through this blog.

If you found this post useful please leave a comment below!