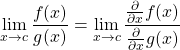Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

List of Important Math for DSP

November 3, 2021

Introduction

The is a list of math for DSP I have found to be useful over my career in DSP. This post will be updated periodically.

Cross-Correlation

Discrete-Time Cross-Correlation

(1) $\begin{equation*}R_{xy}\left[\tau\right] = \sum_{n=-\infty}^{\infty} x[n]y^*[n-\tau]\end{equation*}$

Discrete-Time Autocorrelation

(2) $\begin{equation*}R_{x}\left[\tau\right] = \sum_{n=-\infty}^{\infty} x[n]x^*[n-\tau]\end{equation*}$

Fourier Transform and Inverse Fourier Transform

Transforms in frequency f (Hertz)

The Fourier transform relates the impulse response $x(t)$ which is continuous in time $t$ and the frequency response X(f) which is continuous in frequency f.

(3) $\begin{equation*}X(f) = \int_{-\infty}^{\infty} x(t) e^{-j 2\pi f t} dt\end{equation*}$

(4) $\begin{equation*}x(t) = \int_{-\infty}^{\infty} X(f) e^{j 2\pi f t} df\end{equation*}$

Transforms in frequency omega (radians per second)

The Fourier transform and inverse Fourier transform can be written with the frequency f in Hertz, or by using $\omega$ which is in radians per second.

(5) $\begin{equation*}X\left(\omega\right) = \int_{-\infty}^{\infty} x(t) e^{-j \omega t} dt\end{equation*}$

(6) $\begin{equation*}x(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} X(f) e^{j \omega t} df\end{equation*}$

Fourier transform references here.

Fourier Transform Pairs

(7) $\begin{equation*}\mathcal{F}\{ x(t) \} = X(f)\end{equation*}$

(8) $\begin{equation*}\mathcal{F} \{x^*(t) \} = X^*(-f)\end{equation*}$

(9) $\begin{equation*}\mathcal{F} \{ x(-t) \} = X(-f)\end{equation*}$

(10) $\begin{equation*}\mathcal{F} \{ x^*(-t) \} = X^*(f)\end{equation*}$

Derivations for (8), (9) and (10) here: Fourier Transform Pairs of Conjugation and Time Reversal

Fourier Transform Properties

Convolution Property

(11) $\begin{equation*} \mathcal{F} \{ x(t) \ast h(t) \} = X(f) \cdot H(f)\end{equation*}$

Derivation for (11) here: Fourier Transform Convolution Property Derivation

Linearity Property

(12) $\begin{equation*}\begin{split}\mathcal{F} \{ x(t) + y(t) \} & = \mathcal{F} \{ x(t) \} + \mathcal{F} \{ y(t) \} \\& = X(f) + Y(f).\end{split}\end{equation*}$

Derivation for (12) here: Fourier Transform Linearity Property Derivation

Discrete-Time Fourier Transform and Inverse Transform

The discrete-time Fourier transform relates the impulse response x[n] which is discrete in time n and the frequency response $X\left(e^{j\omega}\right)$ which is continuous in frequency $\omega$ .

(13) $\begin{equation*}X\left(e^{j\omega}\right) = \sum_{n=-\infty}^{\infty} x[n] e^{-j\omega n}\end{equation*}$

(14) $\begin{equation*}x[n] = \frac{1}{2\pi} \int_{-\pi}^{\pi} X(e^{j\omega}) e^{j\omega n} ~ d\omega\end{equation*}$

Trigonometric Identities

(15) $\begin{equation*}e^{j\phi} = \text{cos}(\phi) + j \cdot \text{sin} (\phi)\end{equation*}$

(16) $\begin{equation*}cos(\phi) = \frac{1}{2} \left( e^{j\phi} + e^{-j\phi} \right)\end{equation*}$

(17) $\begin{equation*}sin(\phi) = \frac{1}{2j} \left( e^{j\phi} - e^{-j\phi} \right)\end{equation*}$

Derivation for (16) and (17) here: Using Euler’s Formula to Derive Sine and Cosine

Calculus

Integration by Parts

Reference

(18) $\begin{equation*}\int_{\alpha}^{\beta} u ~ dv = u \cdot v \Big|_{\alpha}^{\beta} - \int_{\alpha}^{\beta} v ~ du\end{equation*}$

Derivatives

(19) $\begin{equation*}\frac{\partial}{\partial x} \text{sin}( x ) = \text{cos}(x)\end{equation*}$

(20) $\begin{equation*}\frac{\partial}{\partial x} \text{cos}( x ) = -\text{sin}(x)\end{equation*}$

L'Hopital's Rule