Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Time Invariant and Time Varying Filters

September 3, 2021

Introduction

The response of time invariant filters is independent of time and have filter weights which do not change over time. Time invariance (TI) is a nice quality for filters to have when analyzing them mathematically and have many applications in which adaptation is not needed. Time-varying filters (TV) are common in radio receivers such as equalizers, automatic gain control and polyphase filters. For example an equalizer is time-varying because the filter weights are dependent on previous input samples. Understanding TI filters is necessary for having a proper DSP foundation before moving onto TV filters.

Time Invariant FIR Filters

The output of a finite pulse response (FIR) filter h[n] is represented by convolution,

(1) $\begin{equation*}y[n] = x[n] \circledast h[n],\end{equation*}$

or alternatively,

(2) $\begin{equation*}\begin{split}y[n] & = \sum_{k=-\infty}^{\infty} x[k] h[n-k] \\& = \sum_{k=-\infty}^{\infty} x[n-k] h[k].\end{split}\end{equation*}$

Figure 1 is an example of a FIR filter.

From(2) it can be seen that x[k] is time reversed, x[-k], and delayed by n samples,

(3) $\begin{equation*}x[n-k] = x[-k+n] = x[-(k-n)].\end{equation*}$

Mathematically either x[n] or h[n] could be time reversed and delayed and the same output would be produced. However for easier analysis the convolution will be implemented by time reversing and delaying x[n].

Expanding (2),

(4) $\begin{equation*}\begin{split}y[n] = \dots + h[-2]x[n+2] + h[-1]x[n+1] + h[0]x[n] + h[1]x[n-1] + \dots ~.\end{split}\end{equation*}$

Delaying x[n] by T samples and substituting into (4) results in

(5) $\begin{equation*}\begin{split}x[n-T] \circledast h[n] = \dots & + h[-2]h[n+2-T] + h[-1]x[n+1-T] + h[0]x[n-T] \\& + h[1]x[n-1-T] + h[2]x[n-2-T]\dots,\end{split}\end{equation*}$

which can be simplified as

(6) $\begin{equation*}y[n-T] = \sum_{k=-\infty}^{\infty} x[k-T] h[n-k],\end{equation*}$

and

(7) $\begin{equation*}y[n-T] = x[k-T] \circledast h[n].\end{equation*}$

From (7) it can be seen that a delay in x[k] by T samples, x[k-T], results in a delay of the output y[n] by T samples, y[n-T] with no other affects. Figure 2 shows how a delay on an input signal results in the same delay in the output when filtered by a time-invariant FIR filter.

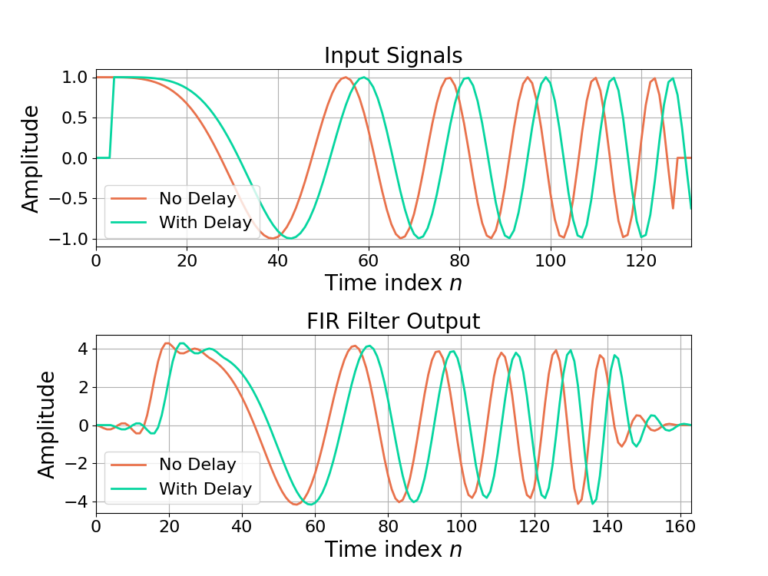
Time Invariant IIR Filters

IIR filters are implemented using a difference equation

(8) $\begin{equation*}y[n] = b_{0}x[n] + b_{1}x[n-1] + \dots + a_{1}y[n-1] + a_{2}y[n-2] + \dots\end{equation*}$

which can be written closed-form as

(9) $\begin{equation*}y[n] = \sum_{k=0}^{K-1} \left( b_{k}x[n-k] + \sum_{p=1}^{P-1} {a_{p}y[n-p] \right)\end{equation*}$

where K are the total number of b coefficients in the feed-forward portion and P-1 are the total number of a coefficients in the feed-back portion.

An example of an IIR filter is given in Figure 3.

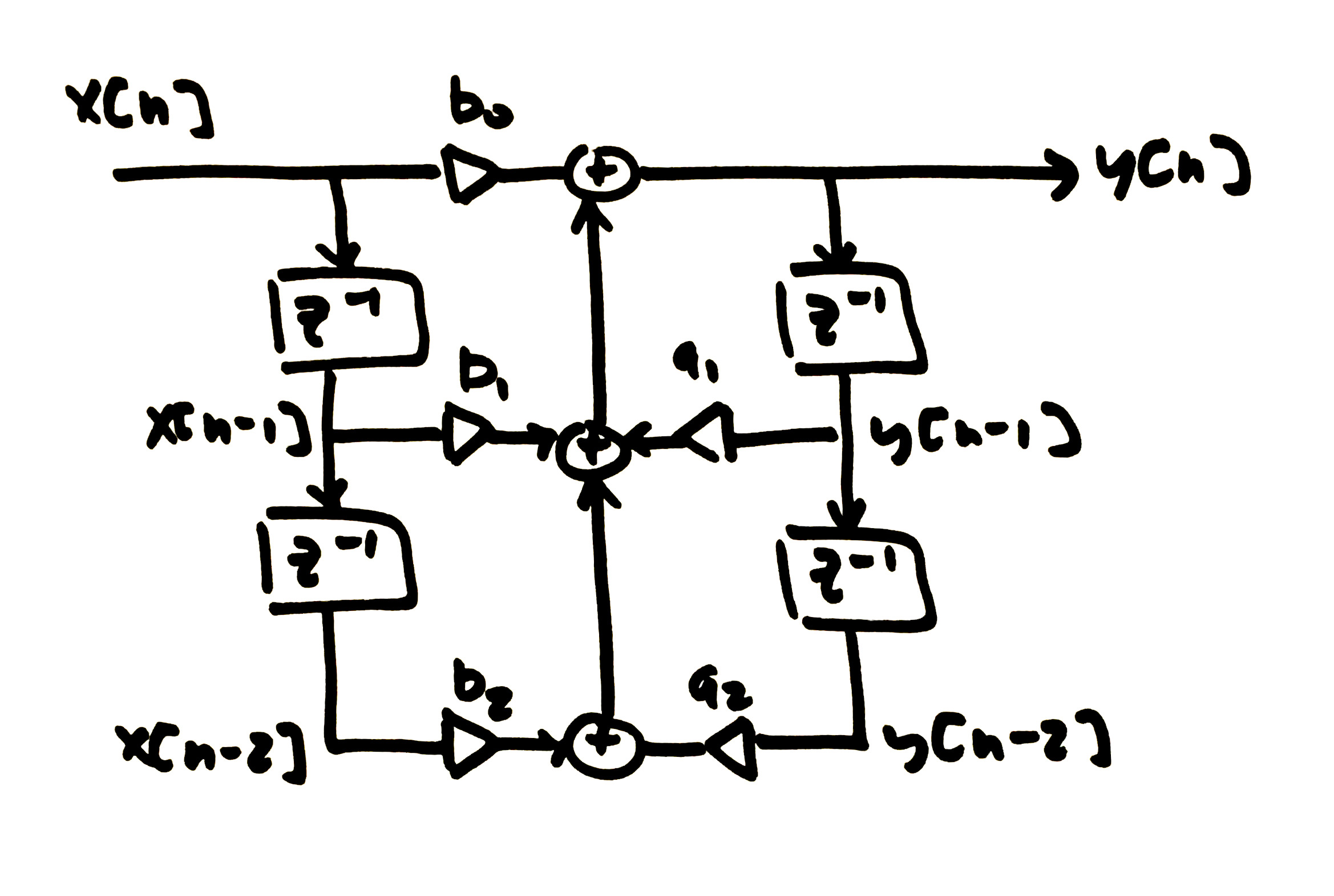
Delaying x[n] by T samples, x[n-T], such that $n \rightarrow n-T$ and substituting into (9) results in

(10) $\begin{equation*}y[n-T] = \sum_{k=0}^{K-1} \left( b_{k}x[n-k-T] + \sum_{p=1}^{P-1} {a_{p}y[n-p-T] \right).\end{equation*}$

From (10), delaying x[n] by T results in the output being delayed by the same amount, y[n-T], with no other impact. The output y[n] is dependent on the input x[n] and the filter weights ak and bp. The filter weights ak and bp are constant for all time and therefore will not being time-varying. A delay of x[n] therefore corresponds directly to a delay in y[n]. Figure 4 gives an example of time-invariance in an IIR filter.

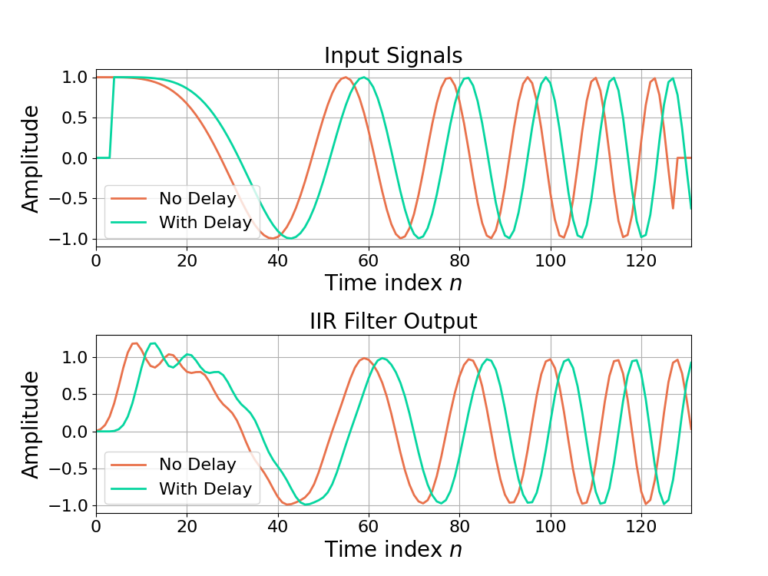
Time-Varying Filters

A decimating FIR filter is a simple case of a time-varying filter. A basic decimation operation is performed by first low-pass filtering and then downsampling, shown in Figure 5.

Combining the low-pass filtering with the downsampling operation will reveal the time-varying nature of the filtering operation and will produce computational efficiencies, referred to as a polyphase decimating filter. The low-pass filter output $\bar{y}[n]$ can be written as

(11) $\begin{equation*}\begin{split}\bar{y}[n] & = x[n] \circledast h[n] \\& = \sum_{k} x[n-k]h[k].\end{split}\end{equation*}$

Downsampling by 2 discards every other sample. Mathematically, it allows for the opportunity to select even indices,

(12) $\begin{equation*}y[n] = \bar{y}[2n]\end{equation*}$

or odd indices,

(13) $\begin{equation*}y[n] = \bar{y}[2n+1].\end{equation*}$

Both (12) and (13) are valid and only differ by delaying the input to the downsample by 1 sample. Choosing

(14) $\begin{equation*}\bar{y}[2n]\end{equation*}$

and substituting (12) into (11) gives

(15) $\begin{equation*}\bar{y}[2n] = \sum_{k} x[2n-k] h[k].\end{split}\end{equation*}$

The filter h[n] produces a single output $\bar{y}[n]$ for each input x[n]. However, the downsampling by 2 operation discards all of the odd indices $\bar{y}[2n+1]$ wasting the computation. The filter h[n] will be rearranged into a polyphase structure to avoid wasting the computation and making the decimation more efficient.

The filter output is arranged into even time indices x[2n] and odd time indices x[2n+1].

(16) $\begin{equation*}\begin{split}\bar{y}[2n] & = \sum_{k ~ \text{even}} x[2n-k]h[k] + \sum_{k ~ \text{odd}} x[2n-k]h[k] \\& = \sum_{k} x[2(n-k)]h[2k] + \sum_{k} x[2(n-k)+1]h[2k-1] \\& = \sum_{k} x[2(n-k)]h[2k] + x[2(n-k)+1]h[2k-1] \\\end{split}\end{equation*}$

From (16) it can be seen that the even input samples x[2(n-k)] are filtered by the even filter weights h[2k] while the odd input samples x[2(n-k)+1] are filtered by the odd filter weights h[2k-1]. The time index of the input samples x[n] therefore indicates which set of filter weights will be applied. Figure 6 gives the polyphase partitioning and shows how the input switch for x[n] controls which filter weights will be applied.

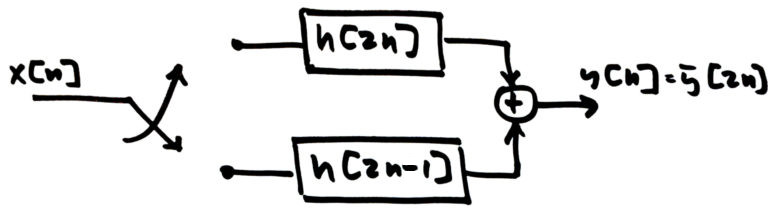
The polyphase decimating filter is therefore periodically time-varying as it produces different filter responses based on the time delay of the input signal. Figure 7 gives an example of how the PTV nature of the polyphase decimating filter affects delays on the input signal.

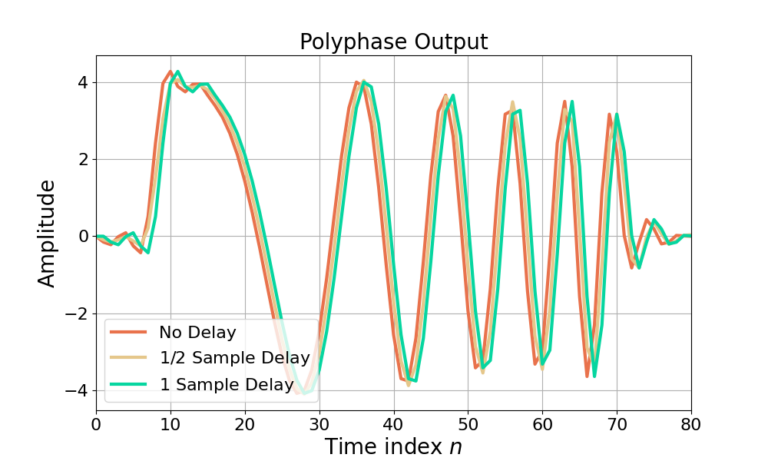
Note that the decimate by 2 polyphase filter is periodically time-varying (PTV) with a period of 2 samples. Figure 7 shows that delaying the input signal by 0 and 2 samples results in the same output signal but with a 1 sample delay. The two-path polyphase filter has a period of 2 samples, meaning a delay of 0, 2, 4, 8, … samples will always pass through the filters h[n] and h[2n-1] in the same order, and therefore will be delayed versions of one another.

Conversely, delaying the input sample by 1 sample produces a different filter response and results in a 1/2 sample delay. A delay of 1, 3, 5, 7, … etc. will send the input samples into filters h[n] and h[2n-1] in the same order, and therefore will be delayed versions of one another.

However, even delays and odd delays will force the input samples to fed into the filters differently, and therefore the even and odd responses will not be delayed version of one another, but instead will have a different impulse response due to the input samples being effected by the weights in a different order. In this way, this gathering of even delays are themselves time-invariant, and the gathering of themselves are also time-invariant. Additionally, because there are two sets of time-invariant outputs, the filter itself is periodically time-varying with a period of 2 samples.

Other Examples of Time Varying Filters

A subset of time-varying filters include adaptive filters whose filter weights are effected by previous samples of the input signal. Such adaptive filters include equalizers and automatic gain control. Another class of time-varying filters are periodically time varying filters which includes polyphase filters.

Conclusion

Delaying the input to a time invariant filter produces the same delay of the output signal with no other modifications. Time-invariant filters have mathematically useful properties for filter analysis and also form the basis for more sophisticated time-varying filters. A polyphase decimating filter is an example of a periodically time-varying filter because the filter response depends on the time delay of the input signal.