Wave Walker DSP

DSP Algorithms for RF Systems

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

DFT Frequency Resolution Explained

March 16, 2022

Introduction

Frequency resolution is defined as the ability to perfectly distinguish one frequency from another. The DFT frequency resolution is improved by increasing the signal length, not increasing the DFT size. The frequency resolution $\omega_{res}$ in radians of the DFT is

(1) $\begin{equation*}\omega_{res} = \frac{2\pi}{N}\end{equation*}$

where N is the length of the input signal.

In this blog I demonstrate graphically and mathematically why and how increasing the signal length improves the frequency resolution, and why simply increasing the DFT size does not.

More blogs on DSP:

Discrete Fourier Transform (DFT)

The discrete-Fourier transform (DFT) translates the time-domain x[n] into the frequency domain X[k]. The number k refers to the $k^{th}$ frequency bin of the frequency domain. The frequency domain X[k] contains information about the amplitude $|X[k]|$ and $\sphericalangle{X[k]}$ phase of the complex sinusoids in the time-domain signal x[n]. The DFT is given by

(2) $\begin{equation*}X[k] = \sum_{n=0}^{N-1} x[n]e^{-j2\pi k n/N}\end{equation*}$

where N is the length of the signal x[n]. The $k^{th}$ frequency bin represents the $2\pi k/N$ .

4-point DFT Frequency Resolution Math

What is the frequency resolution of the DFT? Let’s start with a simpler case and ask the question, what is the frequency resolution of a 4-point DFT X[k] taken over x[n] which is 4 samples long?

Let’s answer a series of questions to get us to the answer. What does frequency resolution mean? Consider this as: what frequencies can be perfectly distinguished by the 4-point DFT? The DFT can perfectly distinguish frequencies when the energy from a signal resides only in a single frequency bin and does not smear into adjacent bins.

Continuing down this path we can also ask: what signals contain content at a single frequency? Recall that the Fourier transform of a complex sinusoid with frequency $\omega_{c}$ is [oppenheim1999, p.62]

(3) $\begin{equation*}X_{c}\left( e^{j\omega} \right) = 2 \pi \delta \left( \omega - \omega_{c} \right),\end{equation*}$

therefore a complex sinusoid is a signal which has information content at a single frequency.

The next question: what frequency (or frequencies) of the complex sinusoid $\omega_{c}$ correspond to the frequencies that can be perfectly resolved by the 4-point DFT? The DFT is able to perfectly estimate frequencies $2\pi k/N$ which are the frequencies of the complex sinusoid in (2). The frequency of the complex sinusoid $\omega_{c}$ is set equivalent to the DFT frequencies,

(4) $\begin{equation*}\omega_c = \frac{2\pi k}{N}.\end{equation*}$

Substituting N=4 into (4),

(5) $\begin{equation*}\omega_c = \frac{2 \pi k}{4} = \frac{\pi}{2} k.\end{equation*}$

The bin index is defined as k = 0, 1, 2, 3 therefore the frequencies $\omega_c$ of the complex exponential which can be perfectly resolved by the 4-point DFT are $0, \pi/2, \pi, 3\pi/2$ .

The frequency resolution of the 4-point DFT is the difference between two adjacent frequencies, for example

(6) $\begin{equation*}3\pi/2 - \pi = \pi/2.\end{equation*}$

The frequency resolution can be written as a normalized frequency by dividing (6) by the sampling frequency in radians (which is $2\pi$ ),

(7) $\begin{equation*}\frac{\pi}{2} \cdot \frac{1}{2\pi} = \frac{1}{4},\end{equation*}$

which is equivalent to one-quarter the sampling frequency $f_s/4$ in Hz.

DFT Frequency Resolution Graphical Example

Let’s consider the same question about frequency resolution of the 4-point DFT from a graphical perspective. Figures 1-4 show the time domain for the complex exponentials and the magnitude of their corresponding frequency responses. All of the time-domain plots give the underlying “CT” or continuous-time complex sinusoid for illustrative purposes. The “DT” is the 4-sample discrete time complex sinusoid.

Figures 1-4 show that the 4-point DFT can perfectly resolve or distinguish the four different complex sinusoids. The frequency resolution is $\pi/2$ , which is normalized to $f_s/4$ or $1/4 ^{th}$ the available bandwidth.

Problem with DFT Frequency Resolution

Figure 5 shows the time domain and magnitude of the frequency domain for the complex sinusoid

(8) $\begin{equation*}e^{j2\pi (1.5/4) n}\end{equation*}$

for $n=0, 1, 2, 3$ . Notice that the frequency $2\pi 1.5/4$ does not fall cleanly into one of the bins of the DFT, instead it resides in between X[1] and X[2]. The magnitude of the frequency response shows that the energy is smeared across all of the bins, X[0], X[1], X[2], X[3] because it is below the frequency resolution and it cannot be resolved to a single bin.

Increasing DFT Size

Note that the frequency resolution is not dependent on the DFT size, the frequency resolution is dependent on the signal length!

Let’s confirm this by increasing the DFT size from 4 to 8. The complex sinusoid (8) with frequency $2\pi 1.5/4$ resides between the two bins X[1] and X[2] for the 4-point DFT. So if the DFT size is increased from 4 to 8, there will be twice the amount of bins and one land at frequency $2\pi 1.5/4$ , or for an 8-point DFT, frequency $2\pi 3/8$ .

The input signal has not changed (4 samples), however there are now twice as many bins in the frequency response (8 bins) because the DFT size has been increased. Figure 6 shows time domain and frequency domain when increasing the DFT size to 8.

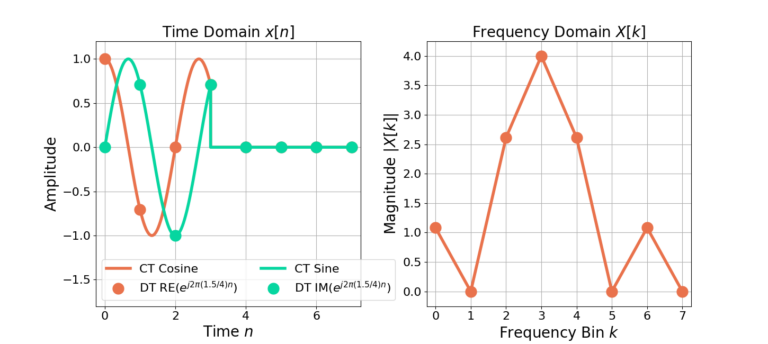
Why is it that increasing the DFT size did not improve the frequency resolution? Figure 6 shows there is now a peak at bin 3 which corresponds to frequency $2\pi 3/8 = 2\pi 1.5/4$ , however there is still the smearing effect across many of the frequencies.

Interpolation versus Resolution

The complex sinusoid (8) with frequency $2\pi 1.5/4$ cannot be resolved by increasing the DFT size. Why? Zero padding in the time domain is applied to take a larger DFT. Since the input signal x[n] is 4 samples long an additional 4 samples of zeros have to be added to the end of the time domain. No new information about the signal has been added, increasing the DFT size simply allows better interpolation between bins but does not improve the frequency resolution.

Think of it this way: you can zoom into an image on a computer screen, but if the image is low-resolution, zooming in (interpolating) will simply give you a bigger pixelated image but will not give you better resolution.

Better DFT Frequency Resolution by Increasing Signal Length

The DFT frequency resolution is dependent on the length of the signal. The complex sinusoid (8) is increased in length from 4 samples to 8 samples and plotted in Figure 7 along with the magnitude of the frequency response from the 8-point DFT.

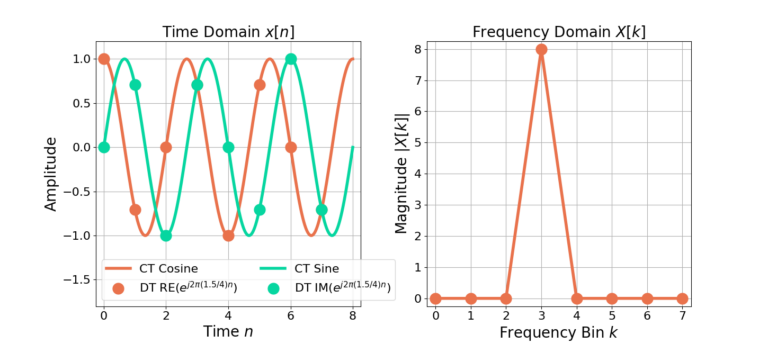
Notice that the complex sinusoid (8) in Figure 7 can now be perfectly resolved to bin k=3, as compared to Figure 6. Increasing the signal length increases the DFT frequency resolution.

Conclusion

The DFT frequency resolution is dependent on the length of the data signal, not the DFT size! Increasing the signal length by a factor of L results in an increase in the frequency resolution by a factor of L. A larger DFT size alone provides more interpolation between bins but does not increase the frequency resolution. Frequency resolution is defined as the ability to perfectly distinguish one frequency from another.