Table of Contents
Introduction
In this post I derive a common trigonometric identity sin(x)^2 + cos(x)^2 = 1 using a form of Euler’s formula.
More blogs on DSP math:
The Identity
(1) ![]()
Trigonometric Identity Derivation
Sine can be written as complex exponentials using a form of Euler’s formula (reference)
(2) ![]()
therefore sine squared is
(3) 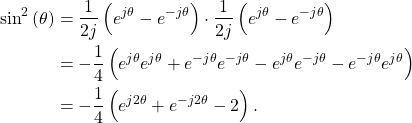
Cosine can be written as complex exponentials using a form of Euler’s formula (reference)
(4) ![]()
therefore cosine squared is
(5) 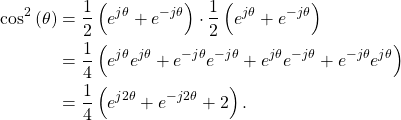
(6) 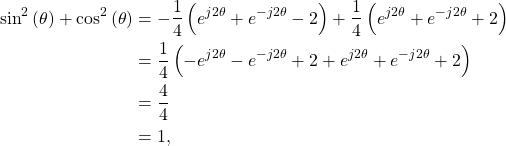
therefore
(7) ![]()
You can find a list of additional trigonometric identities here.
More blogs on DSP math:

![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x100.png)






2 Responses
Hi, really enjoying the site — I’ll be purchasing the book soon enough!
Just wanted to point out that for item (3) it is covering part of the equation and the part that it is covering is missing the 2 from the FOIL, I believe.
Thank you for the comment and great feedback, very much appreciated!
Are you viewing the website on mobile? Try rotating your mobile device to landscape mode. I was able to see (3) on my mobile device once I did that. Also, the -2 comes from the terms – exp(j theta) exp(-j theta) – exp(-j theta) exp(j theta) = -1 -1 = -2.
Feel free to drop me a line at matt@wavewalkerdsp.com after you get a copy of the book, I’d love to get your feedback: what you liked, what you didn’t, and what I can add to the next edition to make it better.