Table of Contents
Introduction
Complex frequency shifting is the process of shifting a signal’s frequency response in the frequency domain. This blog describes how to apply complex frequency shifting in the time domain by multiplication with a complex sinusoid.
A previous blog post described complex frequency conversion in continuous time.
Check out these other blogs!
Complex Frequency Conversion in the Frequency Domain
Complex frequency shifting, or frequency conversion, shifts the frequency response of a signal in the frequency domain. A discrete-time signal ![]() has a frequency response
has a frequency response ![]() related through the Fourier transform,
related through the Fourier transform,
(1) ![]()
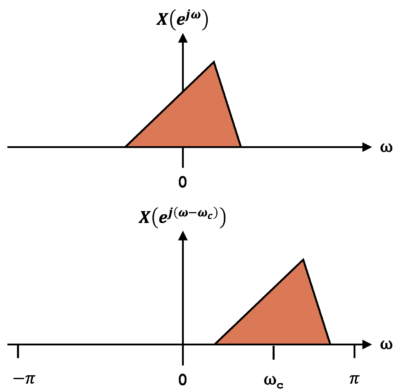
Frequency shifting a frequency response by ![]() is accomplished by substitutting
is accomplished by substitutting
(2) ![]()
such that the frequency response is now
(3) ![]()
Figure 1 demonstrates how complex frequency shifting by ![]() appears in the frequency domain.
appears in the frequency domain.
Discrete-time is only able to represent frequencies
(4) ![]()
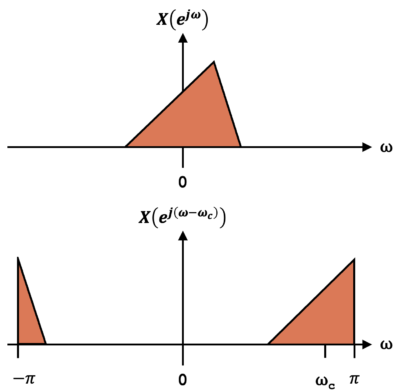
where ![]() is equal to the half sampling rate in radians. Frequency shifting past the half sampling rate can result in aliasing as shown in Figure 2.
is equal to the half sampling rate in radians. Frequency shifting past the half sampling rate can result in aliasing as shown in Figure 2.
Complex Frequency Conversion in the Time Domain
One method of performing frequency shifting is by multiplying the discrete time signal ![]() by a complex sinusoid
by a complex sinusoid
(5) ![]()
resulting in
(6) ![]()
The Fourier transform of (6) is defined by [Oppenheim1999, p.59]
(7) ![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}Z\left( e^{j\omega}\right) & = \mathcal{F} \{ x[n] \cdot y[n] \} \\& = X\left( e^{j\omega}\right) \circledast Y\left( e^{j\omega}\right)\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-c343c8cadbcfb80598f3b2575afaa8aa_l3.png)
where ![]() represents circular convolution. The Fourier transform of (5) is defined as [Oppenheim1999, p.62]
represents circular convolution. The Fourier transform of (5) is defined as [Oppenheim1999, p.62]
(8) ![]()
(9) ![]()
which can be simplified as
(10) ![]()
from the Dirac delta sifting theorem [Oppenheim1999, p.143].
Conclusion
Multiplication of ![]() with
with ![]() shifts the frequency response of
shifts the frequency response of ![]() by
by ![]() , resulting in
, resulting in ![]() .
.
Check out these other blogs!