Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

bookCover2Ed
examples1
examples2
eulersFormula
radians
negativeFrequency
adding
posNegAngles
complexSinusoidPhase
Fourier Transform of the Boxcar Window
July 13, 2022

Table of Contents

Introduction

This blog shows the time domain of the boxcar window, derives it’s frequency response as well as the magnitude-squared of the frequency response.

Check out these other DSP blogs:

Boxcar Window

The boxcar window of length N is defined as

(1)   \begin{equation*}h[n] = \begin{cases}1, & 0 \le n \le N-1 \\0, & \text{otherwise}.\end{cases}\end{equation*}

Equation (1) is plotted in Figure 1 with N=16.

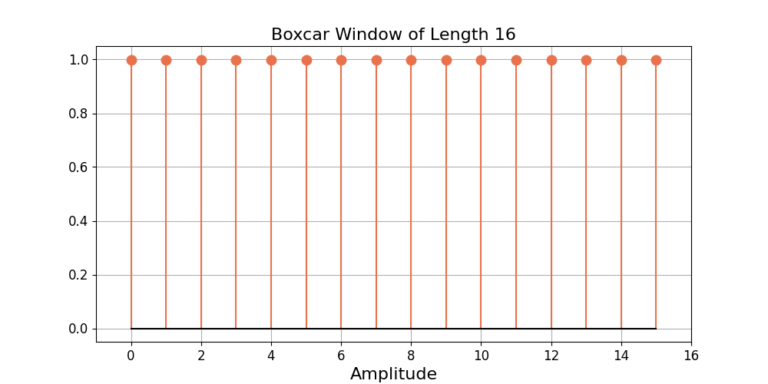
Figure 1: The impulse response of the boxcar window for N=16.
Figure 1: The impulse response of the boxcar window for N=16.

Fourier Transform of Boxcar Window

Since (1) is discrete-time the Discrete-Time Fourier Transform (DTFT) must be taken.

The DTFT is defined as (reference)

(2)   \begin{equation*}X\left(e^{j\omega}\right) = \sum_{n} x[n]e^{-j \omega n}.\end{equation*}

Applying (1) to (2),

(3)   \begin{equation*}\begin{split}H\left( e^{j\omega} \right) & = \sum_{n} h[n] e^{-j\omega n} \\& = \sum_{n=0}^{N-1} e^{-j\omega n}.\end{split}\end{equation*}

Equation (3) is now a finite geometric series. The sum of a finite geometric series

(4)   \begin{equation*}S_L = \sum_{l}^{L-1} a r^{l}\end{equation*}

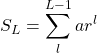
can be written as (reference)

 

(5)   \begin{equation*}S_L = \frac{a \left(1 - r^{L} \right)}{1 - r}.\end{equation*}

Comparing (3) to (4), a = 1 and r = e^{j\omega}. The summation from (5) can therefore be written as

(6)   \begin{equation*}H\left( e^{j\omega} \right) =\frac{1 - e^{-j\omega N}}{1 - e^{-j\omega}}.\end{equation*}

Frequency Response Magnitude

The magnitude-squared of (6) is given by

(7)   \begin{equation*}\begin{split}\left| H\left( e^{j\omega} \right) \right|^2 & = H\left( e^{j\omega} \right) \cdot H^*\left( e^{j\omega} \right) \\& = \frac{1 - e^{-j\omega N}}{1 - e^{-j\omega}} \cdot \frac{1 - e^{j\omega N}}{1 - e^{j\omega}}.\end{split}\end{equation*}

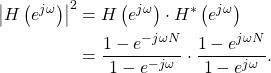
Multiplying the terms from (7),

(8)   \begin{equation*}\left| H\left( e^{j\omega} \right) \right|^2 = \frac{1 + e^{-j\omega N + j\omega N} - e^{-j\omega N} - e^{j\omega N}}{1 + e^{-j\omega +j\omega} - e^{-j\omega} - e^{j\omega}}.\end{equation*}

Gathering like terms,

(9)   \begin{equation*}\left| H\left( e^{j\omega} \right) \right|^2 = \frac{2 - e^{j\omega N} - e^{-j\omega N}}{2 - e^{j\omega} - e^{-j\omega}}.\end{equation*}

The complex exponentials can be written in terms of cosine such that

(10)   \begin{equation*}\left| H\left( e^{j\omega} \right) \right|^2 = \frac{2 - 2 \cos \left( \omega N \right)}{2 - 2 \cos \left( \omega \right)},\end{equation*}

which can be simplified to:

(11)   \begin{equation*}\left| H\left( e^{j\omega} \right) \right|^2 = \frac{1 - \cos \left( \omega N \right)}{1 - \cos \left( \omega \right)}.\end{equation*}

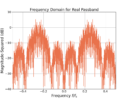
Equation (11) for N=16 is plotted in Figure 2. The computed magnitude is shown along side to show their equivalence and the correctness of the derivation.

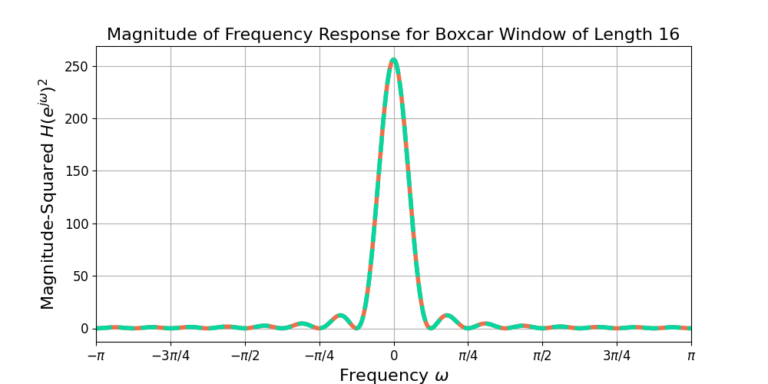
Figure 2: The magnitude-squared of the boxcar window frequency response.
Figure 2: The magnitude-squared of the boxcar window frequency response.

Conclusion

The equation for the boxcar window was given and the frequency response and it’s magnitude-squared was derived. The magnitude-squared of the frequency response was plotted in both equation from and being computed using software to show their equivalence.

Check out these other DSP blogs:

Leave a Reply

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.

© 2021-2023 Wave Walker DSP