Wave Walker DSP

DSP Algorithms for RF Systems

Brand New Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

Previous image

Next image

Single Pole IIR Filter Frequency Response

July 6, 2022

Introduction

This blog post demonstrates how to find the frequency response of the single pole IIR filter and then plots the magnitude and phase responses for multiple $\alpha$ values.

Check out these other blogs on DSP:

Single Pole IIR Impulse Response

The single pole infinite impulse response (IIR) filter is an incredibly efficient filter!

The impulse response of the single pole IIR is

(1) $\begin{equation*}y[n] = \alpha x[n] + (1-\alpha)y[n-1]\end{equation*}$

The filter uses two weights, $\alpha$ and $1-\alpha$ . The weight $\alpha$ is applied to the input signal x[n] and the value is typically small ( $\alpha$ < 0.1 ). The weight $1-\alpha$ is much larger than $\alpha$ and is applied to the feedback y[n-1]. The smaller the $\alpha$ the more impact the feedback has on the output and the smoother (and more narrowband) the filter.

The single pole IIR may also be referred to as an exponential moving average (EMA) filter.

Single Pole IIR Frequency Response

The Z-transform is applied to (1),

(2) $\begin{equation*}Y(z) = \alpha X(z) + (1-\alpha) Y(z)z^{-1}.\end{equation*}$

Equation (2) is simplified by gathering like terms,

(3) $\begin{equation*}Y(z) - (1-\alpha)Y(z)z^{-1} = \alpha X(z),\end{equation*}$

(4) $\begin{equation*}Y(z)(1 - (1-\alpha)z^{-1}) = \alpha X(z).\end{equation*}$

The transfer function for (1) is written as the ratio of Y(z) to X(z),

(5) $\begin{equation*}H(z) = \frac{Y(z)}{X(z)} = \frac{\alpha}{1 - (1-\alpha)z^{-1}}\end{equation*}$

The frequency response $H\left( e^{j\omega}\right)$ is created by substituting

(6) $\begin{equation*}z=e^{j\omega}\end{equation*}$

into (5) resulting in

(7) $\begin{equation*}H\left(e^{j\omega}\right) = \frac{\alpha}{1 - (1-\alpha)e^{-j\omega}}.\end{equation*}$

Simplify (7) by definining

(8) $\begin{equation*}\beta = 1-\alpha\end{equation*}$

such that the frequency response is now

(9) $\begin{equation*}H\left(e^{j\omega}\right) = \frac{\alpha}{1-\beta e^{-j\omega}}.\end{equation*}$

Magnitude of the Frequency Response

The magnitude of the frequency response (9) is

(10) $\begin{equation*}\left| H\left( e^{j\omega} \right) \right| = \sqrt{ H\left(e^{j\omega})H^*\left(e^{j\omega}\right)}.\end{equation*}$

Substituting (9) into (10),

(11) $\begin{equation*}\left|H\left(e^{j\omega}\right)\right| = \frac{\alpha}{\sqrt{\left(1 - \beta e^{-j\omega}\right)\left(1 - \beta e^{j\omega}\right)}}.\end{equation*}$

Example Plots

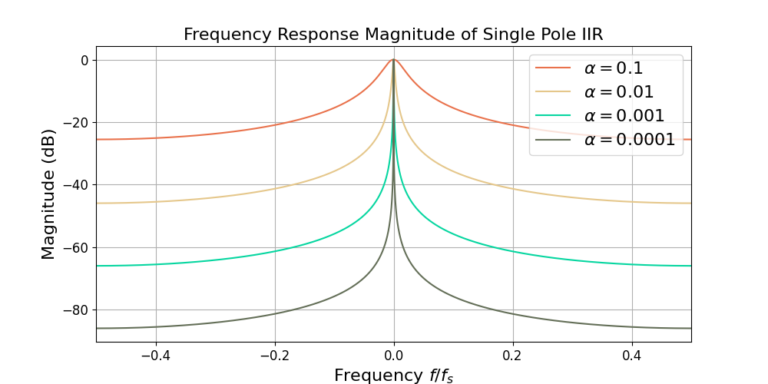
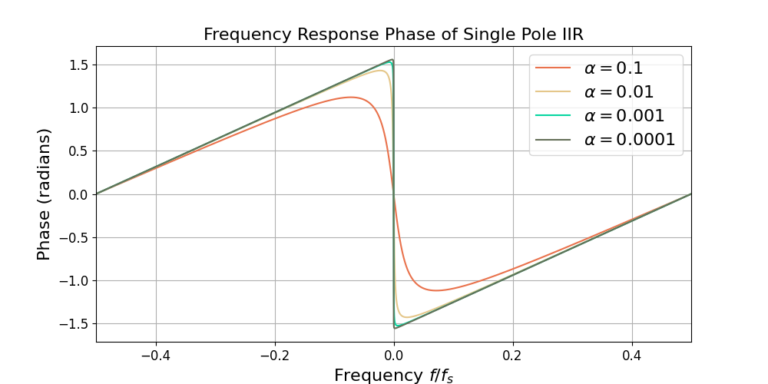
The magnitude and phase of the frequency response (9) is given below. The plots show that as $\alpha$ decreases the filter becomes more narrowband and has more phase linearity.

Conclusion

This blog demonstrated how to find the frequency response of the a single pole IIR filter and plotted the phase and magnitude responses for several $\alpha$ values.

Check out these other blogs on DSP:

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular