Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

bookCover2Ed
examples1
examples2
eulersFormula
radians
negativeFrequency
adding
posNegAngles
complexSinusoidPhase
Band Pass Single Pole IIR Filter Design
February 1, 2023

Table of Contents

Introduction

A low-pass single pole infinite impulse response (IIR) filter is transformed into a band pass filter using simple mathematics!

A previous blog described the frequency response of the single pole IIR filter and how it can be a substitute for a moving average filter.

Don’t miss these other blogs!

Reviewing the Low Pass Filter

A previous blog described how a specific implementation of a single pole IIR filter can be used to approximate a low pass moving average filter. The impulse response of this filter is defined as

(1)   \begin{equation*}y[n] = \alpha x[n] + \left( 1-\alpha\right)y[n-1] \end{equation*}

which may also be referred to as an exponential moving averager or a leaky integrator. The impulse response in (1)

is simplified by setting

(2)   \begin{equation*}\beta = 1-\alpha\end{equation*}

such that

(3)   \begin{equation*}y[n] = \alpha x[n] + \beta y[n-1].\end{equation*}

The frequency response for the low pass filter (LPF) (3) is

(4)   \begin{equation*}H_{LPF}\left( e^{j\omega} \right) = \frac{\alpha}{1-\beta e^{-j\omega}}.\end{equation*}

Transformation into Band Pass Filter

The LPF single pole IIR filter can be transformed into a band pass filter (BPF) through complex frequency shifting. The center frequency of the band pass filter is defined to be \omega_c and the frequency is shifted according to the substitution

(5)   \begin{equation*}\omega \rightarrow \omega - \omega_c.\end{equation*}

The frequency response for the BPF filter is therefore

(6)   \begin{equation*}H_{BPF}\left( e^{j\omega}\right) = H_{LPF}\left( e^{j\left(\omega - \omega_c\right)}\right).\end{equation*}

The LPF frequency response (4) is substituted into (6),

(7)   \begin{equation*}\begin{split}H_{LPF}\left( e^{j\left(\omega - \omega_c\right)} \right) & = \frac{\alpha}{1-\beta e^{-j(\omega - \omega_c)}} \\ & = \frac{\alpha}{1-\beta e^{-j\omega}e^{j\omega_c}}\end{split}\end{equation*}

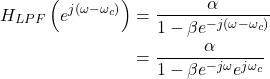
The frequency response is represented using the output Y\left(e^{j\omega}\right) and the input X\left(e^{j\omega}\right)

(8)   \begin{equation*}\begin{split}H_{BPF}\left( e^{j\omega}\right) & = \frac{Y_{BPF}\left( e^{j\omega}\right)}{X_{BPF}\left( e^{j\omega}\right)} \\& = \frac{\alpha}{1-\beta e^{-j\omega}e^{j\omega_c}}\end{split}\end{equation*}

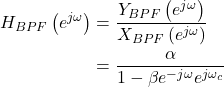
which is rearranged into 

(9)   \begin{equation*}Y_{BPF}\left( e^{j\omega}\right) \left( 1-\beta e^{-j\omega}e^{j\omega_c} \right) = \alpha X_{BPF}\left( e^{j\omega}\right)\end{equation*}

and simplified as 

(10)   \begin{equation*}Y_{BPF}\left( e^{j\omega} \right) - \beta e^{-j\omega}e^{j\omega_c} Y_{BPF}\left( e^{j\omega} \right) = \alpha X_{BPF}\left( e^{j\omega} \right).\end{equation*}

The impulse response is obtained by applying the inverse Z-transform

(11)   \begin{equation*}y[n] - \beta e^{j\omega_c} y[n-1] = \alpha x[n]\end{equation*}

which is more commonly written as

(12)   \begin{equation*}y[n] = \alpha x[n] + \beta e^{j\omega_c} y[n-1].\end{equation*}

The feedback filter coefficient for the LPF is \beta however the bandpass version includes a complex weight \beta e^{j\omega_c}.

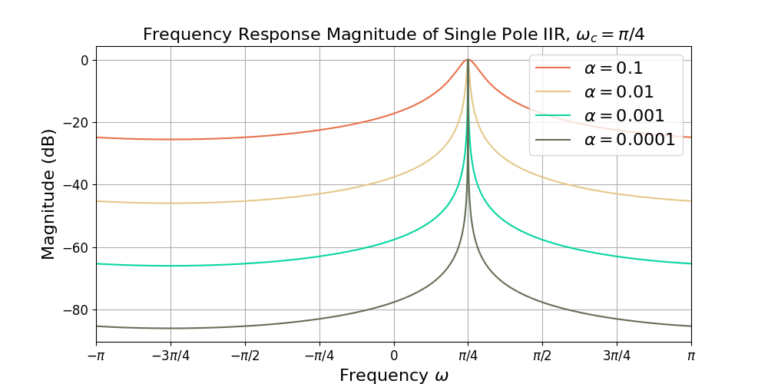
Plotting Examples

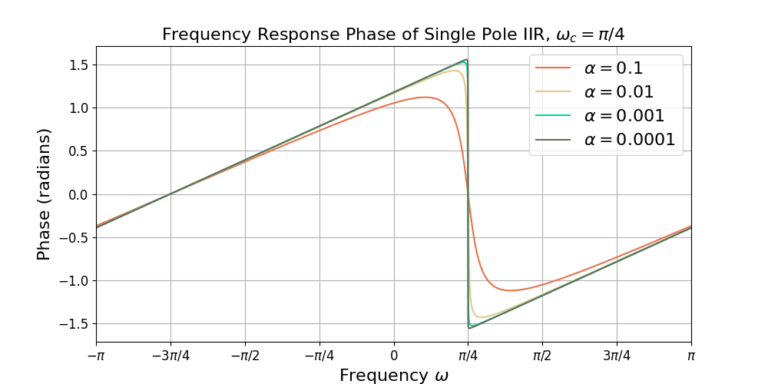
The following plots show the frequency response for the band pass single pole IIR with \omega_c = \pi/4. Figure 1 gives the magnitude of the frequency response and Figure 2 gives the phase of the frequency response. Compare the plots against the LPF in the previous blog post.

Figure 1: Magnitude of the frequency response for the band pass single pole IIR filter.
Figure 1: Magnitude of the frequency response for the band pass single pole IIR filter.
Figure 2: Phase of the frequency response for the band pass single pole IIR filter.

Conclusion

A low-pass single pole IIR filter can be transformed into a band pass through complex frequency shifting. The impulse response for the IIR filter is modified by using a complex exponential as the feedback filter coefficient.

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

Leave a Reply

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.