![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-125x100.png)
Table of Contents
Introduction
An introduction to the Bartlett window: the impulse response is defined and a brief analysis of the frequency response as compared against the rectangular window. The Bartlett may also be referred to as the “triangular” window due to the shape in the time domain.
More blogs!
Bartlett (Triangular) Window Design Equation
The Bartlett window, or triangular window, is a useful tool in spectral analysis. Applying a window function reduces the sidelobes of the spectral response, reducing the energy from higher frequencies that is aliased into the lower frequencies.
The Bartlett window has two forms, both of which produce the equivalent window. The first is [Oppenheim1999, p.468],
(1) ![\begin{equation*}w[n] = \begin{cases}\frac{2n}{N}, & 0 \le n \le N/2, \\2-\frac{2n}{N}, & N/2 < n \le N, \\0, & \text{otherwise,}\end{cases}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-85eebcc072a11aa26112bf6c92e68d00_l3.png "Rendered by QuickLaTeX.com")
where 
is the window length. The second form of the Bartlett window is from NumPy’s function,
(2) ![\begin{equation*}w[n] = \frac{2}{N-1}\left( \frac{N-1}{2} - \left| n - \frac{N-1}{2} \right|\right),\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-72af841784c9549baef5912f304921c1_l3.png "Rendered by QuickLaTeX.com")
where 
. The weights can also be generated using the following python code:
import numpy as np
def createBartlett ( N ):
n = np.arange(0,(N/2))
leftSide = n/((N-1)/2)
if (np.mod(N,2) == 0):
rightSide = leftSide[::-1]
else:
rightSide = leftSide[0:-1][::-1]
window = np.concatenate((leftSide,rightSide))
return window
Impulse Response
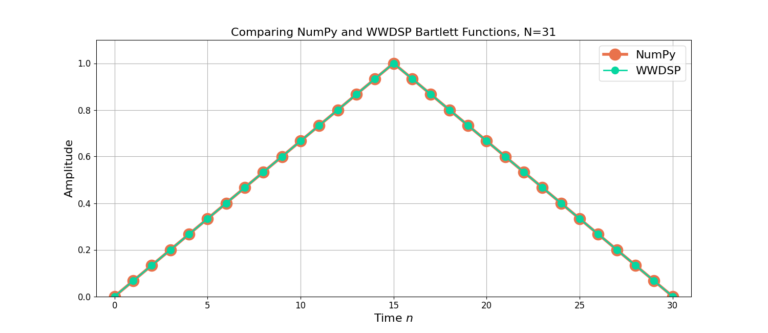
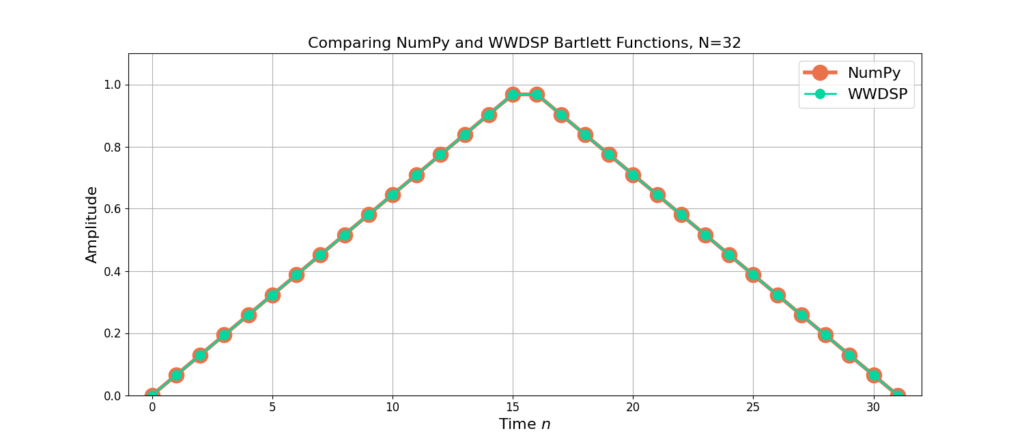
The impulse response for the Bartlett window with length N=31 is given in Figure 1 and length N=32 in Figure 2.
Frequency Domain Analysis
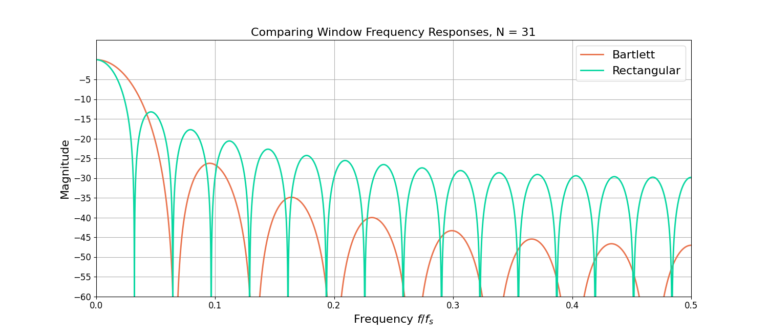
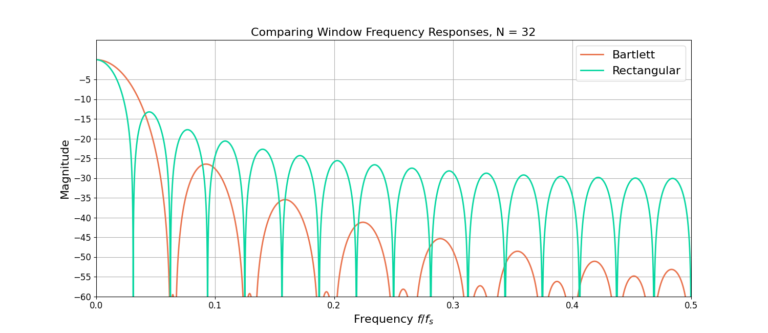
Figures 3 and 4 give the frequency response of the Bartlett window for lengths N=31 and N=32. The rectangular window is used as a comparison because it is the same as not using any windowing function.
The Bartlett window improves the sidelobes by more than 15 dB in Figure 3 and more than 20 dB in Figure 4.
The Bartlett window has two downsides:
- Additional computations to apply the window,
- Increases the bandwidth of the main lobe.
However the improvement in sidelobe attenuation is well worth the cost and produces an overall superior spectral response.
Conclusion
The Bartlett window improves upon the frequency response of the rectangular window by reducing the sidelobes at the cost of increasing the bandwidth of the main lobe and additional computations needed to apply the window. However, the Bartlett window creates a better spectral response than the rectangular window, which is equivalent to applying no window at all.
More blogs!