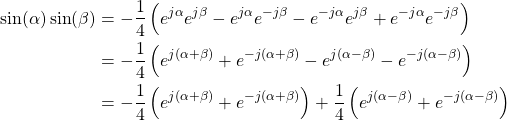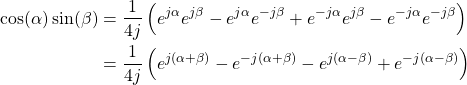Wave Walker DSP

DSP Algorithms for RF Systems

Trending

New Book!

Now for sale: The third edition of DSP for Beginners: Simple Explanations for Complex Numbers! Includes a new chapter on sampling.

DSP for Beginners cover
Euler's formula
Negative frequency in complex sinusoids
Complex sinusoids on the complex plane
Aliasing
Phase relationship between sine and cosine
Product to Sum Trigonometric Identities with Euler’s Formula
June 15, 2022

Table of Contents

Introduction

This blog derives the product to sum trigonometric identities using Euler’s formula,

(1)   \begin{equation*}\cos (\alpha) \cos (\beta) = \frac{1}{2} \left( \cos (\alpha + \beta) + \cos (\alpha - \beta) \right)\end{equation*}

(2)   \begin{equation*}\sin (\alpha) \sin(\beta) = \frac{1}{2} \left( \cos(\alpha - \beta) - \cos (\alpha - \beta) \right),\end{equation*}

(3)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( \sin( \alpha + \beta) - \sin (\alpha - \beta) \right).\end{equation*}

More blogs on DSP Math:

cos(a) cos(b)

Start by substituting Euler’s formula in for both cosine terms,

(4)   \begin{equation*}\cos ( \alpha ) \cos ( \beta ) = \frac{1}{2} \left( e^{j\alpha} + e^{-j\alpha} \right) \cdot \frac{1}{2} \left( e^{j\beta} + e^{-j\beta} \right)\end{equation*}

Multiplying the right hand terms of (4),

(5)   \begin{equation*}\begin{split}\cos ( \alpha ) \cos ( \beta ) & = \frac{1}{4} \left( e^{j\alpha}e^{j\beta} + e^{j\alpha}e^{-j\beta} + e^{-j\alpha}e^{j\beta} + e^{-j\alpha}e^{-j\beta} \right) \\& = \frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} + e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right).\end{split}\end{equation*}

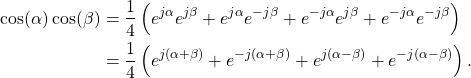
Simplifying (5) with Euler’s formula results in

(6)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) = \frac{1}{2} \cos (\alpha + \beta),\end{equation*}

(7)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \cos ( \alpha - \beta),\end{equation*}

such that

(8)   \begin{equation*}\cos (\alpha) \cos (\beta) = \frac{1}{2} \left( \cos(\alpha + \beta) + \cos (\alpha - \beta) \right).\end{equation*}

sin(a) sin(b)

Start by substituting Euler’s formula in for both sine terms,

(9)   \begin{equation*}\sin(\alpha) \sin(\beta) = \frac{1}{2j} \left( e^{j\alpha} - e^{-j\alpha} \right) \cdot \frac{1}{2j} \left( e^{j\beta} - e^{-j\beta} \right).\end{equation*}

Multiplying the right hand terms of (9),

(10)   \begin{equation*}\begin{split}\sin(\alpha) \sin(\beta) & = -\frac{1}{4} \left( e^{j\alpha}e^{j\beta} - e^{j\alpha}e^{-j\beta} - e^{-j\alpha}e^{j\beta} + e^{-j\alpha}e^{-j\beta} \right) \\& = -\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} - e^{j(\alpha - \beta)} - e^{-j(\alpha - \beta)} \right) \\& = -\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) + \frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) \\\end{split}\end{equation*}

Simplifying (10) with Euler’s formula results in

(11)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) = \frac{1}{2} \cos (\alpha + \beta),\end{equation*}

(12)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \cos ( \alpha - \beta),\end{equation*}

such that

(13)   \begin{equation*}\sin(\alpha) \sin(\beta) = \frac{1}{2} \left( \cos(\alpha - \beta) - \cos(\alpha + \beta) \right).\end{equation*}

cos(a) sin(b)

Start by substituting Euler’s formula in for cosine and sine,

(14)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( e^{j\alpha} + e^{-j\alpha} \right) \cdot \frac{1}{2j} \left( e^{j\beta} - e^{-j\beta} \right).\end{equation*}

Multiplying the right hand terms of (14),

(15)   \begin{equation*}\begin{split}\cos (\alpha) \sin(\beta) & = \frac{1}{4j} \left( e^{j\alpha}e^{j\beta} - e^{j\alpha}e^{-j\beta} + e^{-j\alpha}e^{j\beta} - e^{-j\alpha}e^{-j\beta} \right) \\& = \frac{1}{4j} \left( e^{j(\alpha+\beta)} - e^{-j(\alpha+\beta)} - e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) \\\end{split}\end{equation*}

Simplifying (15) with Euler’s formula results in

(16)   \begin{equation*}\frac{1}{4j} \left( e^{j(\alpha+\beta)} - e^{-j(\alpha+\beta)} \right) = \frac{1}{2} \sin( \alpha + \beta),\end{equation*}

(17)   \begin{equation*}\frac{1}{4j} \left( e^{j(\alpha - \beta)} - e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \sin (\alpha - \beta),\end{equation*}

such that

(18)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( \sin( \alpha + \beta) - \sin (\alpha - \beta) \right).\end{equation*}

Conclusion

The product to sum trigonometric identities were proven using Euler’s formula. 

More blogs on DSP Math:

Leave a Reply

For everything there is a season, and a time for every matter under heaven. A time to cast away stones, and a time to gather stones together. A time to embrace, and a time to refrain from embracing. Ecclesiastes 3:1,5
The earth was without form and void, and darkness was over the face of the deep. And the Spirit of God was hovering over the face of the waters. Genesis 1:2
Behold, I am toward God as you are; I too was pinched off from a piece of clay. Job 33:6
Enter His gates with thanksgiving, and His courts with praise! Give thanks to Him; bless His name! Psalm 100:4
Lift up your hands to the holy place and bless the Lord! Psalm 134:2
Blessed is the man who trusts in the Lord, whose trust is the Lord. He is like a tree planted by water, that sends out its roots by the stream, and does not fear when heat comes, for its leaves remain green, and is not anxious in the year of drought, for it does not cease to bear fruit. Jeremiah 17:7-8
He said to him, “You shall love the Lord your God with all your heart and with all your soul and with all your mind. This is the great and first commandment. And a second is like it: You shall love your neighbor as yourself. On these two commandments depend all the Law and the Prophets.” Matthew 22:37-39
Then He said to me, “Prophesy over these bones, and say to them, O dry bones, hear the word of the Lord. Thus says the Lord God to these bones: Behold, I will cause breath to enter you, and you shall live." Ezekiel 37:4-5
Riches do not profit in the day of wrath, but righteousness delivers from death. Proverbs 11:4
The angel of the Lord appeared to him in a flame of fire out of the midst of a bush. He looked, and behold, the bush was burning, yet it was not consumed. And Moses said, “I will turn aside to see this great sight, why the bush is not burned.” When the Lord saw that he turned aside to see, God called to him out of the bush, “Moses, Moses!” And he said, “Here I am.” Exodus 3:2-3
Daniel answered and said: “Blessed be the name of God forever and ever, to whom belong wisdom and might. He changes times and seasons; He removes kings and sets up kings; He gives wisdom to the wise and knowledge to those who have understanding." Daniel 2:20-21
Now the Lord is the Spirit, and where the Spirit of the Lord is, there is freedom. 2 Corinthians 3:17

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.

© 2021-2025 Wave Walker DSP