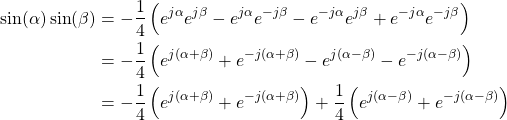Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

bookCover2Ed
examples1
examples2
eulersFormula
radians
negativeFrequency
adding
posNegAngles
complexSinusoidPhase
Product to Sum Trigonometric Identities with Euler’s Formula
June 15, 2022

Table of Contents

Introduction

This blog derives the product to sum trigonometric identities using Euler’s formula,

(1)   \begin{equation*}\cos (\alpha) \cos (\beta) = \frac{1}{2} \left( \cos (\alpha + \beta) + \cos (\alpha - \beta) \right)\end{equation*}

(2)   \begin{equation*}\sin (\alpha) \sin(\beta) = \frac{1}{2} \left( \cos(\alpha - \beta) - \cos (\alpha - \beta) \right),\end{equation*}

(3)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( \sin( \alpha + \beta) - \sin (\alpha - \beta) \right).\end{equation*}

More blogs on DSP Math:

cos(a) cos(b)

Start by substituting Euler’s formula in for both cosine terms,

(4)   \begin{equation*}\cos ( \alpha ) \cos ( \beta ) = \frac{1}{2} \left( e^{j\alpha} + e^{-j\alpha} \right) \cdot \frac{1}{2} \left( e^{j\beta} + e^{-j\beta} \right)\end{equation*}

Multiplying the right hand terms of (4),

(5)   \begin{equation*}\begin{split}\cos ( \alpha ) \cos ( \beta ) & = \frac{1}{4} \left( e^{j\alpha}e^{j\beta} + e^{j\alpha}e^{-j\beta} + e^{-j\alpha}e^{j\beta} + e^{-j\alpha}e^{-j\beta} \right) \\& = \frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} + e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right).\end{split}\end{equation*}

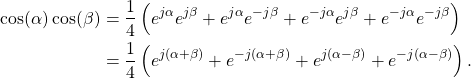
Simplifying (5) with Euler’s formula results in

(6)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) = \frac{1}{2} \cos (\alpha + \beta),\end{equation*}

(7)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \cos ( \alpha - \beta),\end{equation*}

such that

(8)   \begin{equation*}\cos (\alpha) \cos (\beta) = \frac{1}{2} \left( \cos(\alpha + \beta) + \cos (\alpha - \beta) \right).\end{equation*}

sin(a) sin(b)

Start by substituting Euler’s formula in for both sine terms,

(9)   \begin{equation*}\sin(\alpha) \sin(\beta) = \frac{1}{2j} \left( e^{j\alpha} - e^{-j\alpha} \right) \cdot \frac{1}{2j} \left( e^{j\beta} - e^{-j\beta} \right).\end{equation*}

Multiplying the right hand terms of (9),

(10)   \begin{equation*}\begin{split}\sin(\alpha) \sin(\beta) & = -\frac{1}{4} \left( e^{j\alpha}e^{j\beta} - e^{j\alpha}e^{-j\beta} - e^{-j\alpha}e^{j\beta} + e^{-j\alpha}e^{-j\beta} \right) \\& = -\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} - e^{j(\alpha - \beta)} - e^{-j(\alpha - \beta)} \right) \\& = -\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) + \frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) \\\end{split}\end{equation*}

Simplifying (10) with Euler’s formula results in

(11)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha + \beta)} + e^{-j(\alpha + \beta)} \right) = \frac{1}{2} \cos (\alpha + \beta),\end{equation*}

(12)   \begin{equation*}\frac{1}{4} \left( e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \cos ( \alpha - \beta),\end{equation*}

such that

(13)   \begin{equation*}\sin(\alpha) \sin(\beta) = \frac{1}{2} \left( \cos(\alpha - \beta) - \cos(\alpha + \beta) \right).\end{equation*}

cos(a) sin(b)

Start by substituting Euler’s formula in for cosine and sine,

(14)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( e^{j\alpha} + e^{-j\alpha} \right) \cdot \frac{1}{2j} \left( e^{j\beta} - e^{-j\beta} \right).\end{equation*}

Multiplying the right hand terms of (14),

(15)   \begin{equation*}\begin{split}\cos (\alpha) \sin(\beta) & = \frac{1}{4j} \left( e^{j\alpha}e^{j\beta} - e^{j\alpha}e^{-j\beta} + e^{-j\alpha}e^{j\beta} - e^{-j\alpha}e^{-j\beta} \right) \\& = \frac{1}{4j} \left( e^{j(\alpha+\beta)} - e^{-j(\alpha+\beta)} - e^{j(\alpha - \beta)} + e^{-j(\alpha - \beta)} \right) \\\end{split}\end{equation*}

Simplifying (15) with Euler’s formula results in

(16)   \begin{equation*}\frac{1}{4j} \left( e^{j(\alpha+\beta)} - e^{-j(\alpha+\beta)} \right) = \frac{1}{2} \sin( \alpha + \beta),\end{equation*}

(17)   \begin{equation*}\frac{1}{4j} \left( e^{j(\alpha - \beta)} - e^{-j(\alpha - \beta)} \right) = \frac{1}{2} \sin (\alpha - \beta),\end{equation*}

such that

(18)   \begin{equation*}\cos (\alpha) \sin(\beta) = \frac{1}{2} \left( \sin( \alpha + \beta) - \sin (\alpha - \beta) \right).\end{equation*}

Conclusion

The product to sum trigonometric identities were proven using Euler’s formula. 

More blogs on DSP Math:

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

Leave a Reply

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.