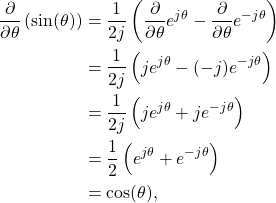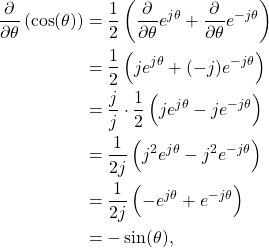Wave Walker DSP

DSP Algorithms for RF Systems

Most Popular

Buy the Book!

DSP for Beginners: Simple Explanations for Complex Numbers! The second edition includes a new chapter on complex sinusoids.

bookCover2Ed
examples1
examples2
eulersFormula
radians
negativeFrequency
adding
posNegAngles
complexSinusoidPhase
Derivative of Sine and Cosine Using Euler’s Formula
April 6, 2022

Table of Contents

Introduction

This posts shows how cosine and sine are related through their derivatives using Euler’s formula. I recall being presented with the derivative of sine and cosine in high school calculus and being asked to accept it on faith. But now I can show you the derivation in simple terms. Enjoy!

Check out these other blogs on DSP math:

For more information check out my book Fundamentals of Digital Signal Processing: Complex Numbers, available on Amazon now!

amazonTitlePage

Derivative of Sine

Sine can be written in terms of complex exponentials (reference),

(1)   \begin{equation*}\sin(\theta) = \frac{1}{2j} \left( e^{j\theta} - e^{-j\theta} \right).\end{equation*}

Taking the derivative of (1),

(2)   \begin{equation*}\frac{\partial}{\partial \theta} \left( \sin (\theta) \right) = \frac{\partial}{\partial \theta} \left( \frac{1}{2j} \left( e^{j\theta} - e^{-j\theta} \right) \right).\end{equation*}

Substituting the derivative

(3)   \begin{equation*}\frac{\partial}{\partial x} e^{ax} = ae^{ax}\end{equation*}

into (2),

(4)   \begin{equation*}\begin{split}\frac{\partial}{\partial \theta} \left( \sin (\theta) \right) & = \frac{1}{2j} \left( \frac{\partial}{\partial \theta} e^{j\theta} - \frac{\partial}{\partial \theta} e^{-j\theta} \right) \\& = \frac{1}{2j} \left( j e^{j\theta} - (-j)e^{-j\theta} \right) \\& = \frac{1}{2j} \left ( je^{j\theta} + je^{-j\theta} \right) \\& = \frac{1}{2} \left ( e^{j\theta} + e^{-j\theta} \right) \\& = \cos(\theta),\end{split}\end{equation*}

therefore

(5)   \begin{equation*}\frac{\partial}{\partial \theta} \left( \sin (\theta) \right) = \cos(\theta).\end{equation*}

Derivative of Cosine

Cosine can be written in terms of complex exponentials (reference),

(6)   \begin{equation*}\cos(\theta) = \frac{1}{2} \left( e^{j\theta} + e^{-j\theta} \right).\end{equation*}

Taking the derivative of (6),

(7)   \begin{equation*}\frac{\partial}{\partial \theta} \left( \cos (\theta) \right) = \frac{\partial}{\partial \theta} \left( \frac{1}{2} \left( e^{j\theta} + e^{-j\theta} \right) \right).\end{equation*}

Substituting (3) into (7),

(8)   \begin{equation*}\begin{split}\frac{\partial}{\partial \theta} \left( \cos (\theta) \right) & = \frac{1}{2} \left( \frac{\partial}{\partial \theta} e^{j\theta} + \frac{\partial}{\partial \theta} e^{-j\theta} \right) \\& = \frac{1}{2} \left( je^{j\theta} + (-j)e^{-j\theta} \right) \\& = \frac{j}{j} \cdot \frac{1}{2} \left( je^{j\theta} - je^{-j\theta} \right) \\& = \frac{1}{2j} \left( j^2 e^{j\theta} - j^2 e^{-j\theta} \right) \\& = \frac{1}{2j} \left( -e^{j\theta} + e^{-j\theta} \right) \\& = -\sin(\theta),\end{split}\end{equation*}

therefore

(9)   \begin{equation*}\frac{\partial}{\partial \theta} \left( \cos (\theta) \right) = -\sin(\theta).\end{equation*}

Conclusion

Much can be done with Euler’s formula, and this is one case of how it can be used to relate sine and cosine through their derivatives. Without Euler’s formula the derivatives can be much, much harder.

Check out these other blogs on DSP math:

 

 

Leave a Reply

God, the Lord, is my strength; he makes my feet like the deer’s; he makes me tread on my high places. Habakkuk 3:19

This website participates in the Amazon Associates program. As an Amazon Associate I earn from qualifying purchases.

© 2021-2023 Wave Walker DSP