Table of Contents
Introduction
This blog performs a simple math derivation for SNR and then verifies the results with a Python simulation.
Check out these DSP blogs!
Calculating SNR Mathematically
An example received signal x[n] is the addition of the signal s[n] and the noise w[n],
(1) ![\begin{equation*}x[n] = s[n] + w[n].\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-98532eecdd7ae16a2cd8fc8e41a7384d_l3.png "Rendered by QuickLaTeX.com")
The SNR of the received signal x[n] is the ratio of the power for the signal 
to the power of the noise 
,
(2) 
where
(3) ![\begin{equation*}P_{s} = \mathbb{E} \{ s[n] s^*[n] \},\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-76448b42aa86c67a7ee8086ddfbf9e5f_l3.png "Rendered by QuickLaTeX.com")
(4) ![\begin{equation*}P_{w} = \mathbb{E} \{ w[n] w^*[n] \}.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-279a9c8a3a7168f53834d0b8a8823196_l3.png "Rendered by QuickLaTeX.com")
The expectation operator 
operates as an average or mean. It is assumed that x[n] is N samples long beginning at time n=0, therefore the average signal power (3) can be written according to
(5) ![\begin{equation*}\begin{split}P_{s} & = \mathbb{E} \{ s[n] s^*[n] \} \\& = \frac{1}{N} \sum_{n=0}^{N-1} s[n] s^*[n] \\& = \frac{1}{N} \sum_{n=0}^{N-1} |s[n]|^2.\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-1a30cac064e0ddcbc5da150fcba0ae88_l3.png "Rendered by QuickLaTeX.com")
Similarly, the average power of the noise (4) is
(6) ![\begin{equation*}P_{w} = \frac{1}{N} \sum_{n=0}^{N-1} |w[n]|^2.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-aaae1bd12f611ee286ba206755469a00_l3.png "Rendered by QuickLaTeX.com")
The SNR of x[n] (2) is therefore [Lyons2011, p.875]
(7) ![\begin{equation*}SNR_{x} = \frac{\frac{1}{N} \sum_{n=0}^{N-1} |s[n]|^2}{\frac{1}{N} \sum_{n=0}^{N-1} |w[n]|^2}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-86dba2066b701592358d12da3974bd94_l3.png "Rendered by QuickLaTeX.com")
which can be written in decibels as
(8) 
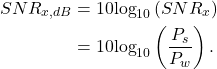
Calculating SNR with Python
Python is used to generate two signals, a BPSK signal and real Gaussian noise. The BPSK signal is generated by the following Python code:
import numpy as np
numSamples = 4096
symbolMap = np.array([-1, 1])
mapIndex = np.random.randint(0,len(symbolMap),numSamples)
symbols = symbolMap[mapIndex]
The average power of the symbols (5) is calculated and printed by:
Ps = np.mean(np.abs(symbolMap)**2)
print('signal power = ' + str(np.round(Ps,2)))
which results in:
signal power = 1.0
The real Gaussian noise is generated by:
noise = np.sqrt(0.01)*np.random.normal(0,1,numSamples)
The average noise power (6) is calculated and printed by:
Pn = np.mean(np.abs(noise)**2)
print('noise power = ' + str(np.round(Pn,2)))
which results in:
noise power = 0.01
The SNR is the ratio of the signal power to the noise power, which is calculated and printed by:
SNRdB = 10*np.log10(Ps/Pn)
print('SNR (dB) = ' + str(np.round(SNRdB)))
which results in:
SNR (dB) = 20.0
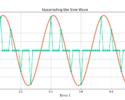
Figure 1 is an example of s[n], w[n] and x[n] in the time domain as generated by the example Python code.
![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/2023/12/HowToComputeSignalToNoiseRatioSNRInSimulation_signalNoiseTimeDomain-768x614.png)
Conclusion
This blog provided a simple mathematical backing for how to compute SNR mathematically and then provided Python code for how to generate an example BPSK and then compute it’s SNR.
Check out these DSP blogs!