Table of Contents
Introduction
Average signal power is important in calculating performance metrics such as signal to noise (SNR) ratio. Read on for how to derive and calculate the average signal power for a finite-length, discrete-time signal. Be sure to check out the post on deriving power and energy for a discrete-time signal.
More DSP blogs:
Signal Power Derivation
The average power of a signal x[n] is defined as
(1) ![]()
The expectation operator ![]() operates as an average or mean. For simplicity, and to make this practical for real-world RF systems, it is assumed that x[n] is N samples long beginning at time n=0. Therefore the expectation from (1) can be expanded according to
operates as an average or mean. For simplicity, and to make this practical for real-world RF systems, it is assumed that x[n] is N samples long beginning at time n=0. Therefore the expectation from (1) can be expanded according to
(2) ![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}P_{x} & = \mathbb{E} \{ x[n] x^*[n] \} \\& = \frac{1}{N} \sum_{n=0}^{N-1} x[n] x^*[n] \\& = \frac{1}{N} \sum_{n=0}^{N-1} |x[n]|^2.\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-0ccc60f6b782e39d2d458308804a7ca4_l3.png)
Examples of Signal Power with Math
Calculating Power with Python
The average power for a complex sinusoid with with amplitude A = 3 is calculated according to (6),
(7) ![]()
Equations (6) and (7) are verified using simulation. The following code creates a complex sinusoid of N=1024 samples with amplitude A = 3 and a random frequency ![]() and then computes the average power:
and then computes the average power:
import numpy as np# build a complex sinusoid A = 3 omega = np.random.uniform(-np.pi,np.pi) n = np.arange(0,1024) complexSinusoid = A*np.exp(1j*omega*n)
# calculate average power
averagePower = np.mean(np.abs(complexSinusoid)**2)
print('avg power = ' + str(np.round(averagePower,2)))
Running the script produces:
avg power = 9.0
which aligns with the mathematical calculation.
Conclusion
This blog describes the average power mathematically, provides a derivation for the average power of a complex sinusoid and verifies the result using a Python simulation.
More DSP blogs:
![A BPSK signal s[n], real Gaussian noise w[n], and the received signal x[n] = s[n] + w[n] for SNR = 20 dB](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/15621-featured-125x100.png)

![Figure 1: The two sequences for the autocorrelation of x0[n] and x0[n].](https://www.wavewalkerdsp.com/wp-content/uploads/wordpress-popular-posts/5515-featured-125x100.png)






![Rendered by QuickLaTeX.com \begin{equation*}x[n] = \begin{cases}A, & 0 \le n < N-1 \\0, & \text{otherwise}.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-c46355470c6070ef155dc4aa6d04f046_l3.png)
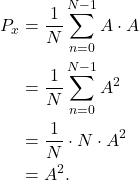
![Rendered by QuickLaTeX.com \begin{equation*}y[n] = \begin{cases}A e^{j\omega n}, & 0 \le n < N-1 \\0, & \text{otherwise}.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-f8e19c6968791b3a645e477c9995c289_l3.png)