Table of Contents
Introduction
This blog describes stationary and cyclostationary processes using simple examples. A stationary process describes when a distribution does not change with time where as a cyclostationary process describes when a distribution changes periodically with time. A forth coming blog will describe the applications of stationarity and cyclostationarity to DSP and RF signals.
Check out these other DSP blogs:
Stationary Process
A stationary process is one whose distribution does not change with time. Stationarity is a characteristic of a probability distribution. A random variable whose distribution does not change with time, or is time-invariant, is referred to as a stationary process.
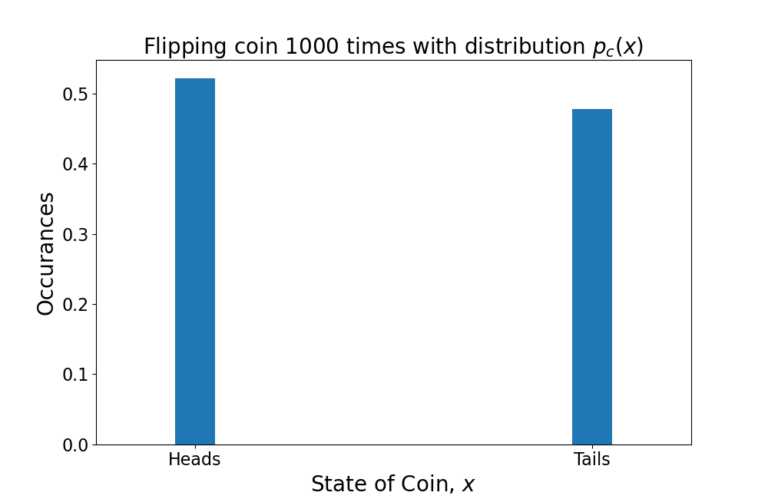
Consider the probability distribution of flipping a coin. The probability of the coin landing on heads is 50% and landing on tails is 50%. The probabilities are the same 100 years ago as they are today and as they will be in 100 years.
Mathematically the probability distribution 
of flipping a coin is described by
(1) 
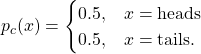
The variable x is the state of the coin. The distribution (1) is time-invariant because time does not factor into the distribution in any way. The distribution is stationary.
Cyclostationary Process
A cyclostationary process is one whose distribution is periodic in time. Cyclostationarity is a characteristic of a probability distribution. A random variable whose distribution changes periodically with time, or is perodically time-varying, is referred to as a cyclostationary process.
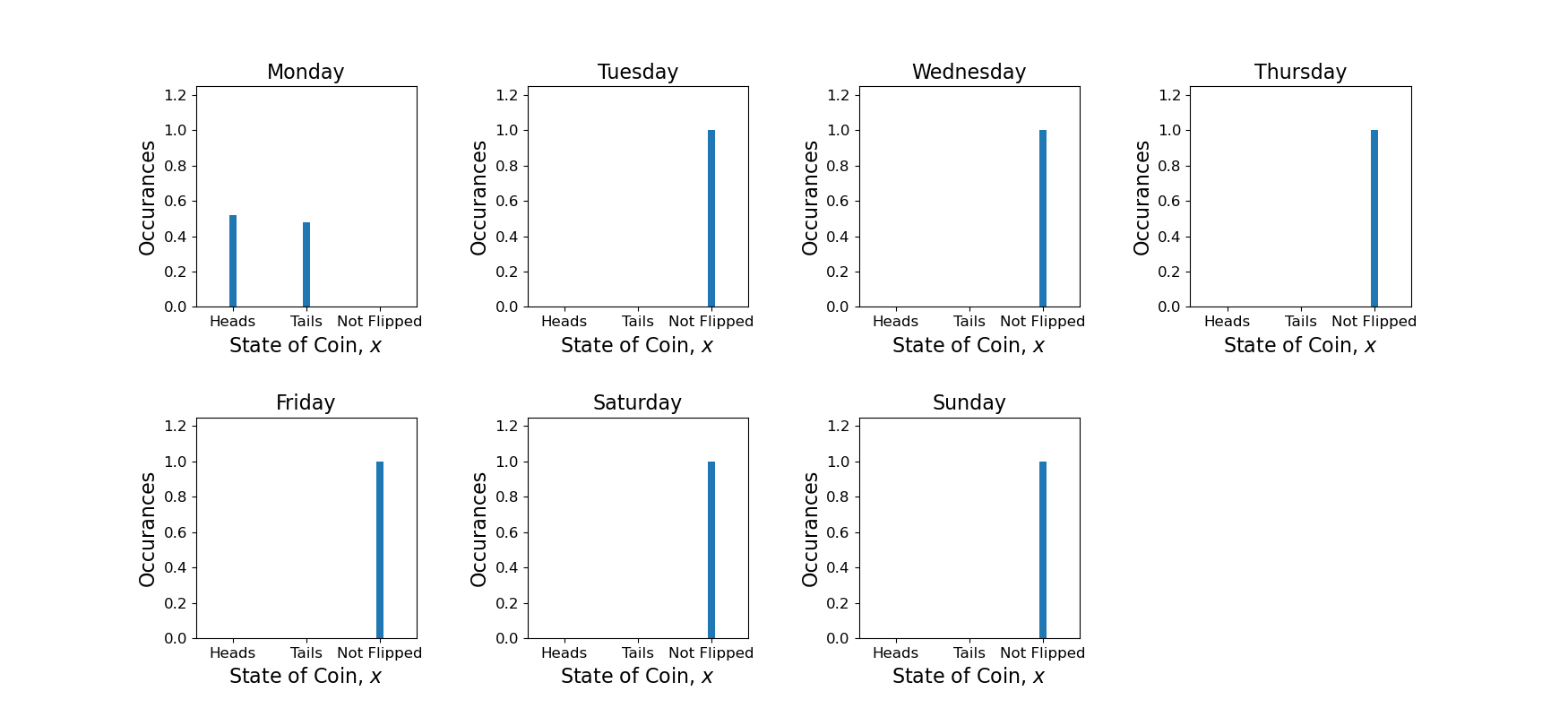
Let’s return to the example of flipping a coin but with a caveat: the coin will only be flipped on Mondays and not flipped all other days of the week.
However, the distribution is periodically time-varying when focusing on each week day individually. For example, the distribution of the coin flip on Monday is defined as
(2) 
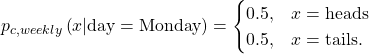
See from (2) that the distribution is stationary, however it occurs every 7 days. A cyclostationary process is one whose distribution is stationary but with a given period which in this case is 7 days.
Continuing the example, the coin flip distribution for Tuesday is defined by
(3) 
Again the distribution (3) is stationary but with a period of every 7 days. The distribution (3) is the same for all other days of the week.
Transforming Cyclostationarity into Stationarity
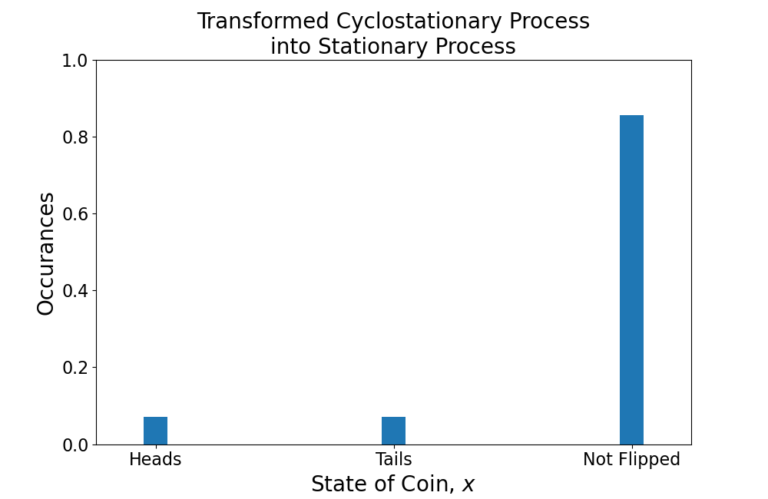
A cyclostationary process can be transformed into a stationary process by averaging out the probabilities across time. This results in distortion because it does not retain the full information about the nature of the cyclostationary process behind the coin flips.
Each day of the week is equally likely, with probability 
. The probability of the coin landing on heads or tails is still 50% but the coin is only flipped once on Mondays, therefore there is a probability of 
the coin landing on heads and probability landing on tails. Since the coin is not flipped 6 out of the 7 days there is a probability of 
that occurring.
The cyclostationary distribution is therefore
(4) 
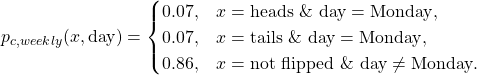
The transformed stationary distribution of the coin is written as
(5) 
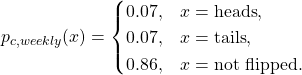
The distribution (5) is stationary because there is no time dependence as compared to (4) which is periodically time-varying. The periodically time-varying nature has been averaged out of the cyclostationary distribution, transforming it into a stationary distribution. This results in a loss of information, or clarity, into the nature of the cyclostationary process.
Conclusion
A stationary process describes when a distribution does not change with time. An example of a stationary process is flipping a coin. A cyclostationary process describes when a distribution changes periodically with time. An example of a cyclostationary process is flipping a coin every Monday.
A forth coming blog will describe the applications of stationarity and cyclostationarity to DSP and RF signals.
Check out these other DSP blogs: