Table of Contents
Introduction
Barker codes are a special type of sequence which have excellent auto-correlation properties. This blog describes Barker codes, gives a mathematically example of the auto-correlation, and lists all of the auto-correlation magnitudes in figures.
Check out these blogs:
Barker Codes
A Barker Code is a sequence of length M whose maximum auto-correlation magnitude at time-lag 
is M, and otherwise the auto-correlation magnitude is less than or equal to 1, such that
(1) ![\begin{equation*}|R_{x}[\tau]| = M,\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-a79945a01cc9c5e94e13426016ee136d_l3.png "Rendered by QuickLaTeX.com")
for and
(2) ![\begin{equation*}|R_{x}[\tau]| \leq 1,\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-6e0a73a591cb14aad4ccf25574ec9866_l3.png "Rendered by QuickLaTeX.com")
for 
.
There are a limited set of Barker codes:
Length 2: [1, -1], [1, 1]
Length 3: [1, 1, -1]
Length 4: [1, 1, -1, 1], [1, 1, 1, -1]
Length 5: [1, 1, 1, -1, 1]
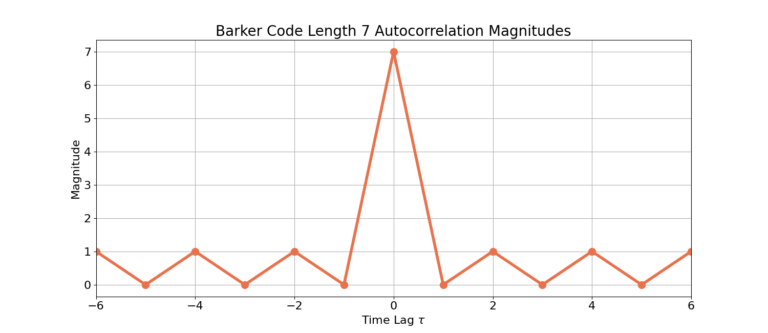
Length 7: [1, 1, 1, -1, -1, 1, -1]
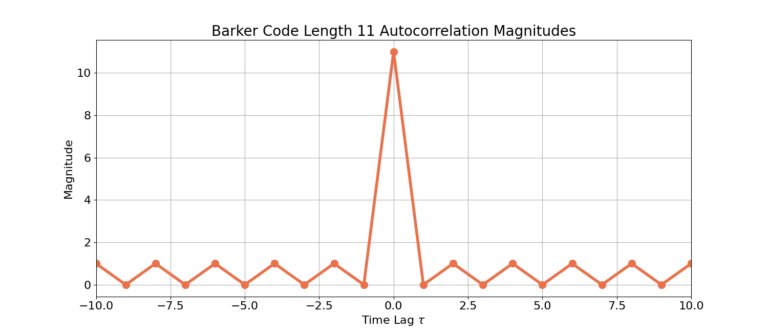
Length 11: [1, 1, 1, -1, -1, -1, -1, 1, -1, -1, 1, -1]
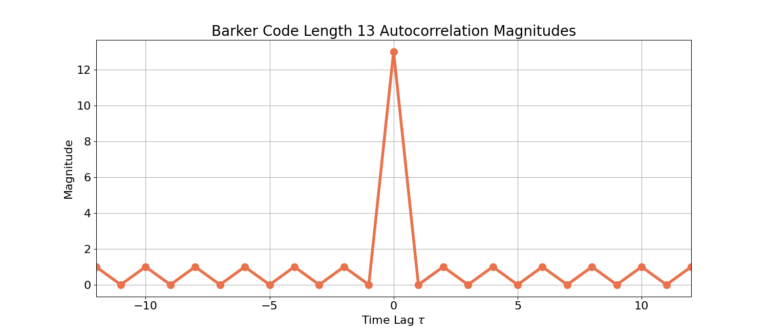
Length 13: [1, 1, 1, 1, 1, -1, -1, 1, 1, -1, 1, -1, 1]
Autocorrelation Mathematically
To demonstrate the auto-correlation properties of a barker code, let us work out an example using the length M=3 code which is 1, 1, -1. For background on autocorrelation, please review the blog: Cross Correlation Explained With Real Signals.
For time delay the two signals will overlap perfectly and the auto-correlation is therefore computed by the element-by-element multiply, summing the result and taking the magnitude:
(3) ![\begin{equation*}|R_{x}[0]| = |(1 \cdot 1) + (1 \cdot 1) + (-1 \cdot -1)| = 3,\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-1d9e171cedf7370a2fee7ecd6c29b29d_l3.png "Rendered by QuickLaTeX.com")
which is equal to the length M=3.
For time delay 
, one signal is delayed by 1 sample and the two sequences are multiplied and summed such that
(4) ![\begin{equation*}|R_{x}[-1]| = |(1 \cdot 0) + (1 \cdot 1) + (-1 \cdot 1)| = 0.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-28bdef9c81779022d235793d2c3c2729_l3.png "Rendered by QuickLaTeX.com")
For time delay 
,
(5) ![\begin{equation*}\begin{split}|R_{x}[-2]| & = |(1 \cdot 0) + (1 \cdot 0) + (-1 \cdot 1)| \\ & = |-1| \\& = 1.\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-a7b35322bd5fbaf30d9fb5a0b890ddba_l3.png "Rendered by QuickLaTeX.com")
For time delay 
,
(6) ![\begin{equation*}|R_{x}[1]| = |(1 \cdot 1) + (1 \cdot -1) + (-1 \cdot 0)| = 0.\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-71f67648557ce81ffb62438819be29f5_l3.png "Rendered by QuickLaTeX.com")
For time delay 
,
(7) ![\begin{equation*}\begin{split}|R_{x}[2]| & = |(1 \cdot -1) + (1 \cdot 0) + (-1 \cdot 0)| \\& = |-1| \\& = 1.\end{split}\end{equation*}](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-7adc8af8426daf123689ec80260b7313_l3.png "Rendered by QuickLaTeX.com")
The auto-correlation magnitude ![|R_{x}[\tau]|](https://www.wavewalkerdsp.com/wp-content/ql-cache/quicklatex.com-d6c80cbbad88569fdcc451238c67bcc4_l3.png "Rendered by QuickLaTeX.com")
is therefore the sequence 1, 0, 3, 0, 1, which can be seen graphically in the following section.
Autocorrelation Plots
The following figures display the auto-correlation magnitudes for all of the Barker codes.
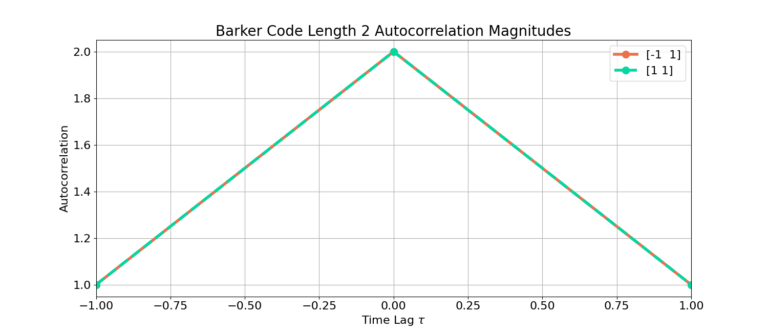
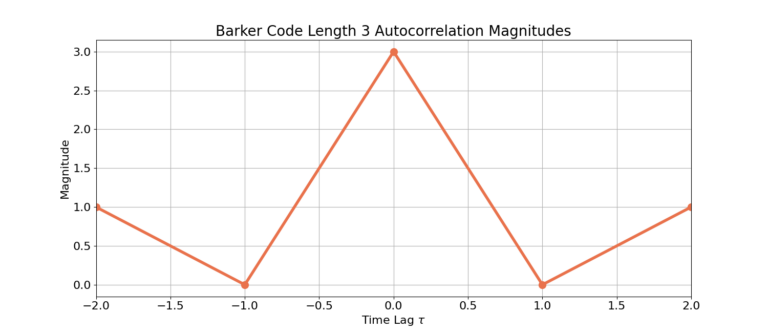
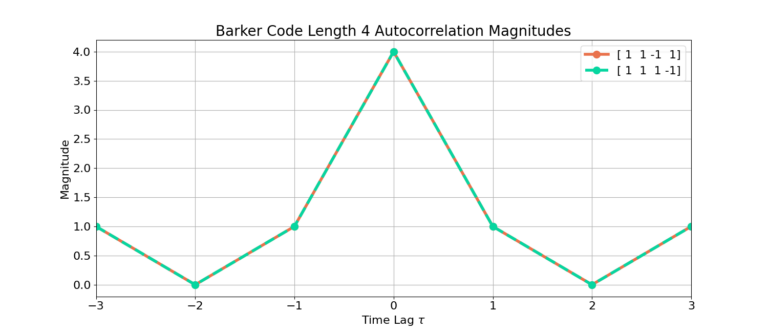
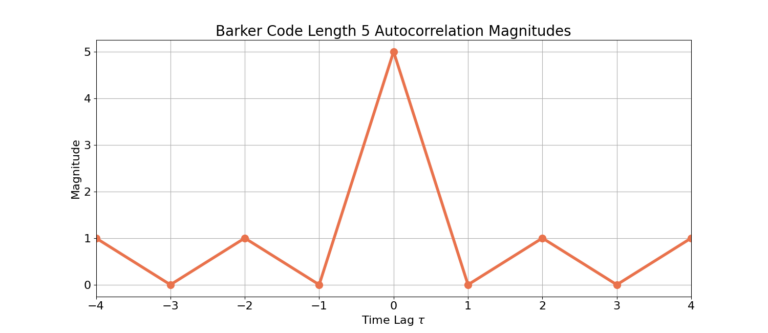
Conclusion
This blog lists the Barker codes, describes and demonstrates their auto-correlation properties mathematically, and displays the auto-correlation magnitudes for all sequences graphically.
Check out these blogs: